365. 水壶问题
- 难度:
中等 - 本题涉及算法:
欧几里得算法(辗转相除法) - 思路:
最大公约数 - 类似题型:
题目 水壶问题
有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升 水。
你允许:
- 装满任意一个水壶
- 清空任意一个水壶
- 从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例
示例 1:
输入: x = 3, y = 5, z = 4
输出: True
示例 2:
输入: x = 2, y = 6, z = 5
输出: False
1. 欧几里得算法(辗转相除法)
这条算法基于一个定理:两个正整数a和b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。比如10和25,25除以10商2余5,那么10和25的最大公约数,等同于10和5的最大公约数。
- 基于这条定理:
首先,我们先计算出a除以b的余数c,把问题转化成求出b和c的最大公约数;然后计算出b除以c的余数d,把问题转化成求出c和d的最大公约数;再然后计算出c除以d的余数e,把问题转化成求出d和e的最大公约数……以此类推,逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算,直到两个数可以整除,或者其中一个数减小到1为止。
欧几里得法(辗转相除法) 通过举例说明
举例: 105和85的最大公约数
- 第一轮计回算 105÷85=1…20
- 第二轮计算 85÷20=4…5
- 第三轮计算 20÷5=4
- 第三轮没有余数, 因此 105和85的最大公约数就是第三轮计算的被除数 5
解题思路
- 求最大公约数 官方叫做 欧几里得法(辗转相除法)
- 代码一目了然,不用文字赘述了
代码
class Solution:
def canMeasureWater(self, a: int, b: int, c: int) -> bool:
# 保证a>b
if b>a:
a , b = b ,a
if c == 0: # 当c == 0 时 肯定满足
return True
if a + b < c: # 这个条件 题目中没说清楚
return False
if b == 0: # 当b=0时 a==c 才能满足条件
return a==c
# 求最大公约数,官方叫法 欧几里得法(辗转相除法)
while b!=0:
temp = a % b
a = b
b = temp
if c%a!=0:
return False
return True
class Solution {
public boolean canMeasureWater(int x, int y, int z) {
if(z==0) { // 当z == 0 时 肯定满足
return true;
}
if(x+y<z) { //这个条件 题目中没说清楚
return false;
}
if (x==0) { // 当x=0时 z==y 才能满足条件
return z==y;
}
// # 保证y>x
if(x>y) {
int c = x;
x = y;
y = c;
}
// 求最大公约数,官方叫法 欧几里得法(辗转相除法)
while (y%x!=0) {
int c = y;
y = x;
x = c%x;
}
return z%x==0;
}
}
before (2020-04-29更新)
自己的思路
- 找到x,y的最大公约数能否z被整除
自己的代码
java
class Solution {
public boolean canMeasureWater(int x, int y, int z) {
boolean b1= false;
boolean b2= false;
boolean b3= false;
if(z==0) {
return true;
}
if(x+y<z) {
return false;
}
if (x==0) {
return z==y;
}
if(x>y) {
int c = x;
x = y;
y = c;
}
while (y%x!=0) {
int c = y;
y = x;
x = c%x;
}
return z%x==0;
}
}
python
class Solution:
def canMeasureWater(self, x, y, z):
"""
:type x: int
:type y: int
:type z: int
:rtype: bool
"""
if z == 0:
return True
if x+y < z:
return False
if x>y:
x,y=y,x
if x == 0:
return y==z
while y%x != 0:
y,x = x,y%x
return z%x==0
用时
两小时
官方解题思路
思路及算法
首先对题目进行建模。观察题目可知,在任意一个时刻,此问题的状态可以由两个数字决定:X 壶中的水量,以及 Y 壶中的水量。
在任意一个时刻,我们可以且仅可以采取以下几种操作:
- 把 X 壶的水灌进 Y 壶,直至灌满或倒空;
- 把 Y 壶的水灌进 X 壶,直至灌满或倒空;
- 把 X 壶灌满;
- 把 Y 壶灌满;
- 把 X 壶倒空;
- 把 Y 壶倒空。 因此,本题可以使用深度优先搜索来解决。搜索中的每一步以 remain_x, remain_y 作为状态,即表示 X 壶和 Y 壶中的水量。在每一步搜索时,我们会依次尝试所有的操作,递归地搜索下去。这可能会导致我们陷入无止境的递归,因此我们还需要使用一个哈希结合(HashSet)存储所有已经搜索过的 remain_x, remain_y 状态,保证每个状态至多只被搜索一次。
在实际的代码编写中,由于深度优先搜索导致的递归远远超过了 Python 的默认递归层数(可以使用 sys 库更改递归层数,但不推荐这么做),因此下面的代码使用栈来模拟递归,避免了真正使用递归而导致的问题。
官方代码
class Solution:
def canMeasureWater(self, x: int, y: int, z: int) -> bool:
stack = [(0, 0)]
self.seen = set()
while stack:
remain_x, remain_y = stack.pop()
if remain_x == z or remain_y == z or remain_x + remain_y == z:
return True
if (remain_x, remain_y) in self.seen:
continue
self.seen.add((remain_x, remain_y))
# 把 X 壶灌满。
stack.append((x, remain_y))
# 把 Y 壶灌满。
stack.append((remain_x, y))
# 把 X 壶倒空。
stack.append((0, remain_y))
# 把 Y 壶倒空。
stack.append((remain_x, 0))
# 把 X 壶的水灌进 Y 壶,直至灌满或倒空。
stack.append((remain_x - min(remain_x, y - remain_y), remain_y + min(remain_x, y - remain_y)))
# 把 Y 壶的水灌进 X 壶,直至灌满或倒空。
stack.append((remain_x + min(remain_y, x - remain_x), remain_y - min(remain_y, x - remain_x)))
return False
复杂度分析
- 时间复杂度:$O(log(min(x, y)))$,取决于计算最大公约数所使用的辗转相除法。
- 空间复杂度:$O(1)$,只需要常数个变量。
一句话概念(python)
- 正负无穷float(‘inf’)的一些用法
- Python3 批量更新模块(包)
- all(iterable) 内置函数 all() 函数用于判断给定的可迭代参数 iterable 中的所有元素是否都为 TRUE,如果是返回 True,否则返回 False。
- 与all(iterable) 与之对于的是 any(iterable)
- python中的循环
- 如果if + for列表的方式同时使用示例
i for i in conf if i > 2 或 if i > 2 for i in conf - python中break、continue 、exit() 、pass终止循环的区别python中break、continue 、exit() 、pass区分 如果您使用嵌套循环,break语句将停止执行最深层的循环,并开始执行下一行代码。
面试题40. 最小的k个数
- 难度:
简单 - 本题涉及算法:
小根堆大根堆快排二叉树 - 思路:
小根堆大根堆}快排暴力二叉树数据范围有限时直接计数排序就行了 - 类似题型:
题目 面试题40. 最小的k个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
方法一 暴力
java
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
for (int i=0;i<arr.length-1;i++) {
if (arr[i]>arr[i+1]){
int temp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = temp;
}
for (int j=i;j>0;j--) {
if(arr[j]<arr[j-1]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
int[] res = new int[k];
for (int i = 0;i<k;i++) {
res[i] = arr[i];
}
return res;
}
}
python
class Solution(object):
def getLeastNumbers(self, arr, k):
"""
:type arr: List[int]
:type k: int
:rtype: List[int]
"""
for i in range(len(arr)-1):
if arr[i]> arr[i+1]:
sort(arr,i)
for j in range(i,0,-1):
if arr[j] < arr[j-1]:
lowsort(arr,j)
return arr[:k]
def sort(arr,i):
temp = arr[i]
arr[i] = arr[i+1]
arr[i+1] = temp
return arr
def lowsort(arr,j):
temp = arr[j]
arr[j] = arr[j-1]
arr[j-1] = temp
return arr
方法二 小根堆
/**
* 小根堆
* @param arr
* @param k
* @return
*/
public int[] getLeastNumbersByStack(int[] arr,int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 默认是小根堆,实现大根堆需要重写一下比较器。
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1); // 目的是最大数在第一位
for(int num :arr) {
if(pq.size()<k)
pq.offer(num);
else if(pq.peek()>num) {
pq.poll();
pq.offer(num);
}
}
// 返回堆中的元素
int[] res = new int[pq.size()];
int idx = 0;
for(int num: pq) {
res[idx++] = num;
}
return res;
}
方法三 大根堆
我们用一个大根堆实时维护数组的前 kk 小值。首先将前 kk 个数插入大根堆中,随后从第 k+1k+1 个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可
class Solution:
def getLeastNumbers(self, nums: List[int], k: int) -> List[int]:
if k == 0: return []
n, opposite = len(nums), [-1 * x for x in nums[:k]]
heapq.heapify(opposite)
for i in range(k, len(nums)):
if -opposite[0] > nums[i]:
# 维持堆大小不变
heapq.heappop(opposite)
heapq.heappush(opposite, -nums[i])
return [-x for x in opposite]
方法三 二叉树
/**
* 二叉树
* @param arr
* @param k
* @return
*/
public int[] getLeastNumbersByTree(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// TreeMap的key是数字, value是该数字的个数。
// cnt表示当前map总共存了多少个数字。
TreeMap<Integer, Integer> map = new TreeMap<>();
int cnt = 0;
for (int num: arr) {
// 1. 遍历数组,若当前map中的数字个数小于k,则map中当前数字对应个数+1
if (cnt < k) {
map.put(num, map.getOrDefault(num, 0) + 1);
cnt++;
continue;
}
// 2. 否则,取出map中最大的Key(即最大的数字), 判断当前数字与map中最大数字的大小关系:
// 若当前数字比map中最大的数字还大,就直接忽略;
// 若当前数字比map中最大的数字小,则将当前数字加入map中,并将map中的最大数字的个数-1。
Map.Entry<Integer, Integer> entry = map.lastEntry();
if (entry.getKey() > num) {
map.put(num, map.getOrDefault(num, 0) + 1);
if (entry.getValue() == 1) {
map.pollLastEntry();
} else {
map.put(entry.getKey(), entry.getValue() - 1);
}
}
}
}
方法五 数据范围有限时直接计数排序就行了:O(N)
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 统计每个数字出现的次数
int[] counter = new int[10001];
for (int num: arr) {
counter[num]++;
}
// 根据counter数组从头找出k个数作为返回结果
int[] res = new int[k];
int idx = 0;
for (int num = 0; num < counter.length; num++) {
while (counter[num]-- > 0 && idx < k) {
res[idx++] = num;
}
if (idx == k) {
break;
}
}
return res;
}
}
方法四 排序
# 这个方法很快,总感觉有作弊嫌疑
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
arr.sort()
return arr[:k]
before (2020-04-29更新)
自己的思路
- 给数组排序
用时
08:08-09:09 (1小时)
代码
public class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (arr[0] >= arr[1]) {
int a = arr[1];
arr[1] = arr[0];
arr[0] = a;
}
a:for (int i = 1; i < arr.length - 1; i++) {
if (arr[i] >= arr[i + 1]) {
int c = arr[i + 1];
arr[i + 1] = arr[i];
arr[i] = c;
for (int j = i; j > 0; j--) {
if (arr[j] <= arr[j - 1]) {
int d = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = d;
continue;
}
continue a;
}
}
}
int[] res = new int[k];
for (int q =0;q<k;q++) {
res[q]=arr[q];
}
return res;
}
}
官方解题思路
方法一:排序
思路和算法
对原数组从小到大排序后取出前 kk 个数即可。
class Solution(object):
def getLeastNumbers(self, arr, k):
"""
:type arr: List[int]
:type k: int
:rtype: List[int]
"""
arr.sort()
return arr[:k]
方法二:堆
比较直观的想法是使用堆数据结构来辅助得到最小的 k 个数。堆的性质是每次可以找出最大或最小的元素。我们可以使用一个大小为 k 的最大堆(大顶堆),将数组中的元素依次入堆,当堆的大小超过 k 时,便将多出的元素从堆顶弹出。我们以数组 [5, 4, 1, 3, 6, 2, 9][5,4,1,3,6,2,9], k=3k=3 为例展示元素入堆的过程,如下面动图所示:
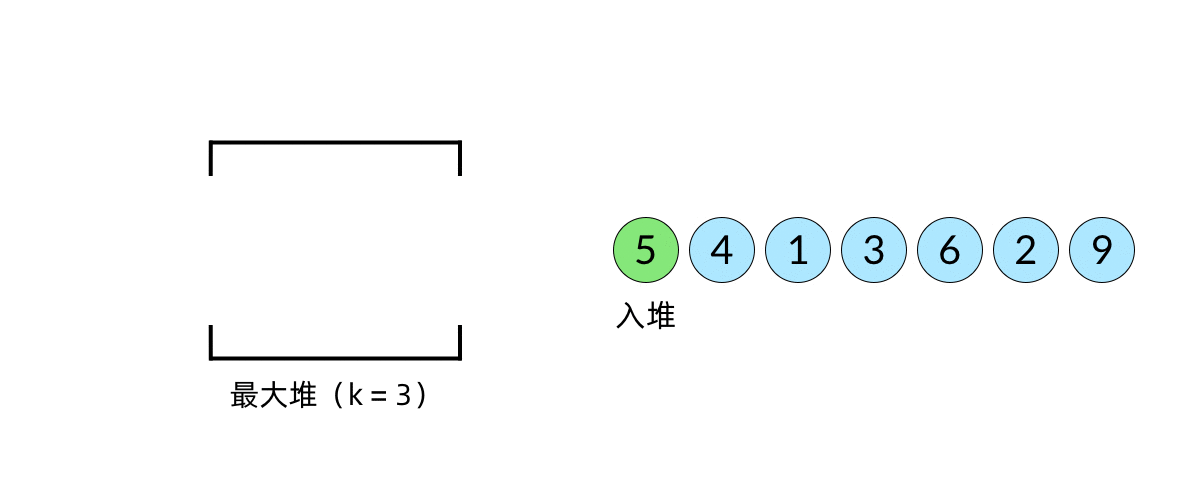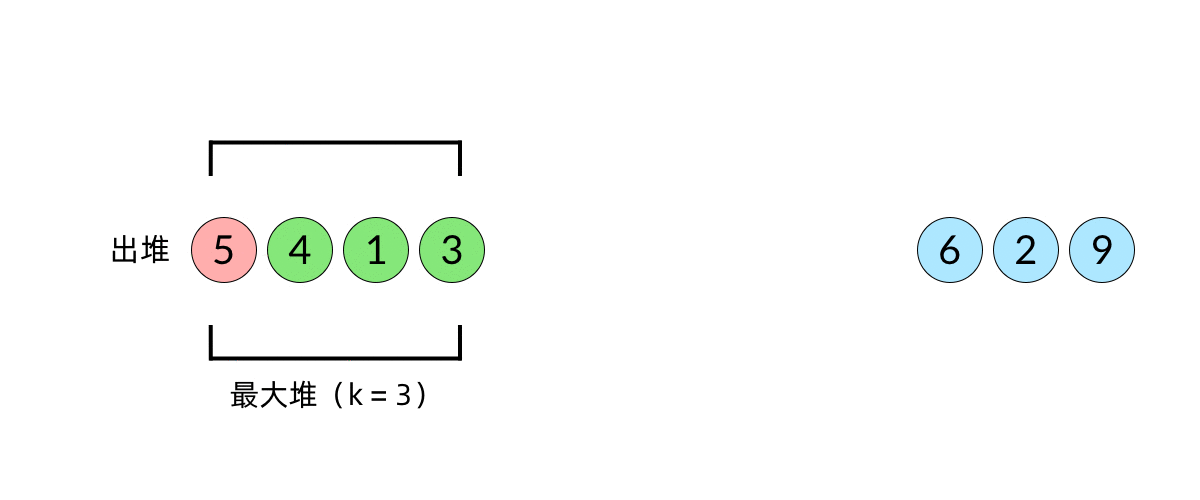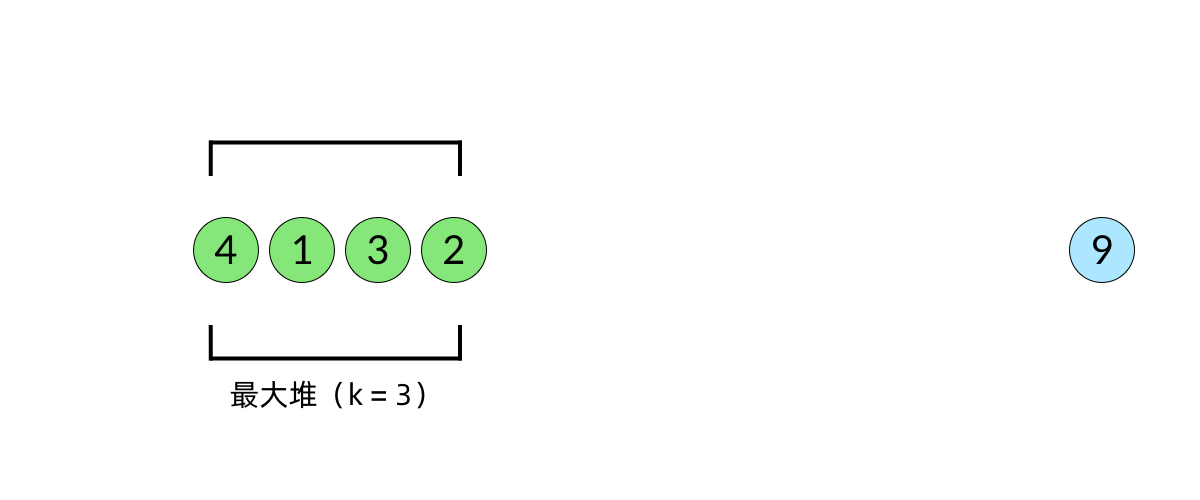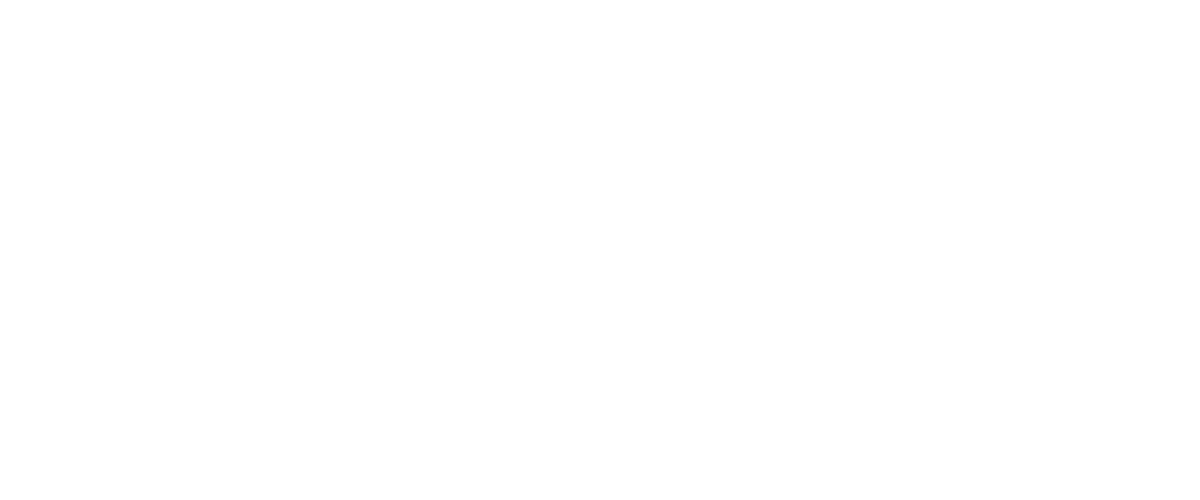
这样,由于每次从堆顶弹出的数都是堆中最大的,最小的 k 个元素一定会留在堆里。这样,把数组中的元素全部入堆之后,堆中剩下的 k 个元素就是最大的 k 个数了。
注意在动画中,我们并没有画出堆的内部结构,因为这部分内容并不重要。我们只需要知道堆每次会弹出最大的元素即可。在写代码的时候,我们使用的也是库函数中的优先队列数据结构,如 Java 中的 PriorityQueue。在面试中,我们不需要实现堆的内部结构,把数据结构使用好,会分析其复杂度即可。
以下是题解代码:
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0) {
return new int[0];
}
// 使用一个最大堆(大顶堆)
// Java 的 PriorityQueue 默认是小顶堆,添加 comparator 参数使其变成最大堆
Queue<Integer> heap = new PriorityQueue<>(k, (i1, i2) -> Integer.compare(i2, i1));
for (int e : arr) {
heap.add(e);
if (heap.size() > k) {
heap.poll(); // 删除堆顶最大元素
}
}
// 将堆中的元素存入数组
int[] res = new int[heap.size()];
int j = 0;
for (int e : heap) {
res[j++] = e;
}
return res;
}
方法三:分治
Top K 问题的另一个分治解法就比较难想到,需要在平时有算法的积累。实际上,“查找第 k 大的元素”是一类算法问题,称为选择问题。找第 k 大的数,或者找前 k 大的数,有一个经典的 quick select(快速选择)算法。这个名字和 quick sort(快速排序)看起来很像,算法的思想也和快速排序类似,都是分治法的思想。
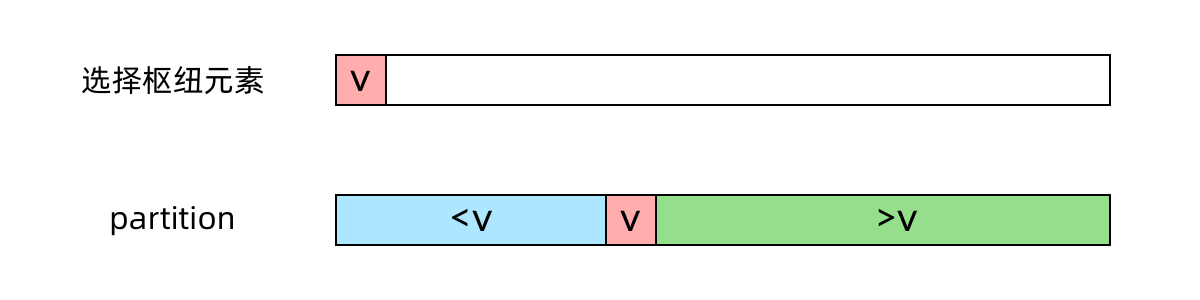
让我们回顾快速排序的思路。快速排序中有一步很重要的操作是 partition(划分),从数组中随机选取一个枢纽元素 v,然后原地移动数组中的元素,使得比 v 小的元素在 v 的左边,比 v 大的元素在 v 的右边,如下图所示:
这个 partition 操作是原地进行的,需要 O(n)O(n) 的时间,接下来,快速排序会递归地排序左右两侧的数组。而快速选择(quick select)算法的不同之处在于,接下来只需要递归地选择一侧的数组。快速选择算法想当于一个“不完全”的快速排序,因为我们只需要知道最小的 k 个数是哪些,并不需要知道它们的顺序。
我们的目的是寻找最小的 kk 个数。假设经过一次 partition 操作,枢纽元素位于下标 mm,也就是说,左侧的数组有 mm 个元素,是原数组中最小的 mm 个数。那么:
- 若 k = mk=m,我们就找到了最小的 kk 个数,就是左侧的数组;
- 若 k<mk<m ,则最小的 kk 个数一定都在左侧数组中,我们只需要对左侧数组递归地 parition 即可;
- 若 k>mk>m,则左侧数组中的 mm 个数都属于最小的 kk 个数,我们还需要在右侧数组中寻找最小的 k-mk−m 个数,对右侧数组递归地 partition 即可。 这种方法需要多加领会思想,如果你对快速排序掌握得很好,那么稍加推导应该不难掌握 quick select 的要领。
以下是题解代码:
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0) {
return new int[0];
} else if (arr.length <= k) {
return arr;
}
// 原地不断划分数组
partitionArray(arr, 0, arr.length - 1, k);
// 数组的前 k 个数此时就是最小的 k 个数,将其存入结果
int[] res = new int[k];
for (int i = 0; i < k; i++) {
res[i] = arr[i];
}
return res;
}
void partitionArray(int[] arr, int lo, int hi, int k) {
// 做一次 partition 操作
int m = partition(arr, lo, hi);
// 此时数组前 m 个数,就是最小的 m 个数
if (k == m) {
// 正好找到最小的 k(m) 个数
return;
} else if (k < m) {
// 最小的 k 个数一定在前 m 个数中,递归划分
partitionArray(arr, lo, m-1, k);
} else {
// 在右侧数组中寻找最小的 k-m 个数
partitionArray(arr, m+1, hi, k);
}
}
// partition 函数和快速排序中相同,具体可参考快速排序相关的资料
// 代码参考 Sedgewick 的《算法4》
int partition(int[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
int v = a[lo];
while (true) {
while (a[++i] < v) {
if (i == hi) {
break;
}
}
while (a[--j] > v) {
if (j == lo) {
break;
}
}
if (i >= j) {
break;
}
swap(a, i, j);
}
swap(a, lo, j);
// a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
方法四 快速排序
思路和用快排求第k大的元素类似,在fastSort方法中,我们并不对每一个元素都进行排序,只需要判断一下分区点和k的值的关系 如果k >p+1 说明 分区点左右的都不需要排序了 因为他们的和小于k
class Solution {
public int[] getLeastNumbers(int [] input, int k) {
fastSort(input,0,input.length-1,k);
int[] res = new int[k];
for(int i = 0 ;i< k;i++){
res[i] = input[i];
}
return res;
}
private void fastSort(int[] a,int s,int e,int k){
if(s > e)return;
int p = partation(a,s,e);
if(p+1 == k){
return;
}else if(p+1 < k){
fastSort(a,p+1,e,k);
}else{
fastSort(a,s,p-1,k);
}
}
private int partation(int[] a,int s ,int e){
int privot = a[e];//取最后一个数作为分区点
int i = s;
for(int j = s;j < e;j++){
if(a[j] < privot){
swap(a,i,j);
i++;
}
}
swap(a,i,e);
return i;
}
private void swap(int[] a ,int i ,int j){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
复杂度分析
-
时间复杂度:O(n\log n),其中 n 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂度。
-
空间复杂度:O(\log n),排序所需额外的空间复杂度为 O(\log n)。
浅析PropertySource 基本使用
示例用法
一、PropertySource 简介
org.springframework.context.annotation.PropertySource 是一个注解,可以标记在类上、接口上、枚举上,在运行时起作用。而@Repeatable(value = PropertySources.class) 表示在PropertySources 中此注解时可以重复使用的。如下:
@Target({ElementType.TYPE})
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Repeatable(PropertySources.class)
public @interface PropertySource {
String name() default "";
String[] value();
boolean ignoreResourceNotFound() default false;
String encoding() default "";
Class<? extends PropertySourceFactory> factory() default PropertySourceFactory.class;
}
二、@PropertySource与Environment读取配置文件
此注解@PropertySource 为Spring 中的 Environment提供方便和声明机制,通常与Configuration一起搭配使用。
- 新建一个maven 项目,添加pom.xml 依赖:
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
<modelVersion>4.0.0</modelVersion>
<groupId>com.spring.propertysource</groupId>
<artifactId>spring-propertysource</artifactId>
<version>0.0.1-SNAPSHOT</version>
<name>spring-propertysource</name>
<description>Demo project for Spring Boot</description>
<properties>
<java.version>1.8</java.version>
<spring.version>4.3.13.RELEASE</spring.version>
</properties>
<dependencies>
<dependency>
<groupId>org.springframework</groupId>
<artifactId>spring-core</artifactId>
<version>${spring.version}</version>
</dependency>
<dependency>
<groupId>org.springframework</groupId>
<artifactId>spring-context</artifactId>
<version>${spring.version}</version>
</dependency>
</dependencies>
<build>
<pluginManagement>
<plugins>
<plugin>
<groupId>org.apache.maven.plugins</groupId>
<artifactId>maven-compiler-plugin</artifactId>
<version>3.2</version>
<configuration>
<source>1.6</source>
<target>1.6</target>
</configuration>
</plugin>
</plugins>
</pluginManagement>
</build>
</project>
- 一般把版本名称统一定义在 标签中,便于统一管理,如上可以通过${…} 来获取指定版本。
- 定义一个application.properties 来写入如下配置
com.spring.name=liuXuan
com.spring.age=18
- 新建一个TestBean,定义几个属性
public class TestBean {
private String name;
private Integer age;
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getAge() {
return age;
}
public void setAge(Integer age) {
this.age = age;
}
@Override
public String toString() {
return "TestBean{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
}
- 新建一个main class ,用来演示@PropertySource 的使用
@Configuration
@PropertySource(value = "classpath:application.properties",ignoreResourceNotFound = false)
public class SpringPropertysourceApplication {
@Resource
Environment environment;
@Bean
public TestBean testBean(){
TestBean testBean = new TestBean();
// 读取application.properties中的name
testBean.setName(environment.getProperty("com.spring.name"));
// 读取application.properties中的age
testBean.setAge(Integer.valueOf(environment.getProperty("com.spring.age")));
System.out.println("testBean = " + testBean);
return testBean;
}
public static void main(String[] args) {
ApplicationContext applicationContext = new AnnotationConfigApplicationContext(SpringPropertysourceApplication.class);
TestBean testBean = (TestBean)applicationContext.getBean("testBean");
}
}
输出:
testBean = TestBean{name='liuXuan', age=18}
Refreshing the spring context
- @Configuration : 相当于 标签,注意不是,一个配置类可以有多个bean,但是只能有一个
- @PropertySource: 用于引入外部属性配置,和Environment 配合一起使用。其中ignoreResourceNotFound 表示没有找到文件是否会报错,默认为false,就是会报错,一般开发情况应该使用默认值,设置为true相当于生吞异常,增加排查问题的复杂性.
- 引入PropertySource,注入Environment,然后就能用environment 获取配置文件中的value值。
三、@PropertySource与@Value读取配置文件
@Value 基本使用
我们以DB的配置文件为例,来看一下如何使用@Value读取配置文件
- 首先新建一个DBConnection,具体代码如下:
// 组件bean
@Component
@PropertySource("classpath:db.properties")
public class DBConnection {
@Value("${DB_DRIVER_CLASS}")
private String driverClass;
@Value("${DB_URL}")
private String dbUrl;
@Value("${DB_USERNAME}")
private String userName;
@Value("${DB_PASSWORD}")
private String password;
public DBConnection(){}
public void printDBConfigs(){
System.out.println("Db Driver Class = " + driverClass);
System.out.println("Db url = " + dbUrl);
System.out.println("Db username = " + userName);
System.out.println("Db password = " + password);
}
}
-
类上加入@Component 表示这是一个组件bean,需要被spring进行管理,@PropertySource 用于获取类路径下的db.properties 配置文件,@Value用于获取properties中的key 对应的value值,printDBConfigs方法打印出来对应的值。
-
新建一个db.properties,具体文件如下
#MYSQL Database Configurations
DB_DRIVER_CLASS=com.mysql.jdbc.Driver
DB_URL=jdbc:mysql://localhost:3306/test
DB_USERNAME=cxuan
DB_PASSWORD=111111
APP_NAME=PropertySourceExample
- 这是一个MYSQL连接数据库驱动的配置文件。
- 新建一个SpringMainClass,用于测试DBConection中是否能够获取到@Value的值
public class SpringMainClass {
public static void main(String[] args) {
AnnotationConfigApplicationContext context = new AnnotationConfigApplicationContext();
// 注解扫描,和@ComponentScan 和 基于XML的配置<context:component-scan base-package>相同
context.scan("com.spring.propertysource.app");
// 刷新上下文环境
context.refresh();
System.out.println("Refreshing the spring context");
// 获取DBConnection这个Bean,调用其中的方法
DBConnection dbConnection = context.getBean(DBConnection.class);
dbConnection.printDBConfigs();
// 关闭容器(可以省略,容器可以自动关闭)
context.close();
}
}
输出:
Refreshing the spring context
Db Driver Class = com.mysql.jdbc.Driver
Db url = jdbc:mysql://localhost:3306/test
Db username = cxuan
Db password = 111111
@Value 高级用法
在实现了上述的例子之后,我们再来看一下@Value 的高级用法:
- @Value 可以直接为字段赋值,例如:
@Value("cxuan")
String name;
@Value(10)
Integer age;
@Value("${APP_NAME_NOT_FOUND:Default}")
private String defaultAppName;
- @Value 可以直接获取系统属性,例如:
@Value("${java.home}")
// @Value("#{systemProperties['java.home']}") SPEL 表达式
String javaHome;
@Value("${HOME}")
String dir;
- @Value 可以注解在方法和参数上
@Value("Test") // 可以直接使用Test 进行单元测试
public void printValues(String s, @Value("another variable") String v) {
...
}
修改DBConnection后的代码如下:
public class DBConnection {
@Value("${DB_DRIVER_CLASS}")
private String driverClass;
@Value("${DB_URL}")
private String dbUrl;
@Value("${DB_USERNAME}")
private String userName;
@Value("${DB_PASSWORD}")
private String password;
public DBConnection(){}
public void printDBConfigs(){
System.out.println("Db Driver Class = " + driverClass);
System.out.println("Db url = " + dbUrl);
System.out.println("Db username = " + userName);
System.out.println("Db password = " + password);
}
}
在com.spring.propertysource.app 下 新增DBConfiguration,作用是配置管理类,管理DBConnection,并读取配置文件,代码如下:
@Configuration
@PropertySources({
@PropertySource("classpath:db.properties"),
@PropertySource(value = "classpath:root.properties", ignoreResourceNotFound = true)
})
public class DBConfiguration {
@Value("Default DBConfiguration")
private String defaultName;
@Value("true")
private boolean defaultBoolean;
@Value("10")
private int defaultInt;
@Value("${APP_NAME_NOT_FOUND:Default}")
private String defaultAppName;
@Value("#{systemProperties['java.home']}")
// @Value("${java.home}")
private String javaHome;
@Value("${HOME}")
private String homeDir;
@Bean
public DBConnection getDBConnection() {
DBConnection dbConnection = new DBConnection();
return dbConnection;
}
@Value("Test") // 开启测试
public void printValues(String s, @Value("another variable") String v) {
System.out.println("Input Argument 1 = " + s);
System.out.println("Input Argument 2 = " + v);
System.out.println("Home Directory = " + homeDir);
System.out.println("Default Configuration Name = " + defaultName);
System.out.println("Default App Name = " + defaultAppName);
System.out.println("Java Home = " + javaHome);
System.out.println("Home dir = " + homeDir);
System.out.println("Boolean = " + defaultBoolean);
System.out.println("Int = " + defaultInt);
}
}
使用SpringMainClass 进行测试,测试结果如下:
Input Argument 1 = Test
Input Argument 2 = another variable
Home Directory = /Users/mr.l
Default Configuration Name = Default DBConfiguration
Default App Name = Default
Java Home = /Library/Java/JavaVirtualMachines/jdk1.8.0_191.jdk/Contents/Home/jre
Home dir = /Users/mr.l
Boolean = true
Int = 10
Refreshing the spring context
Db Driver Class = com.mysql.jdbc.Driver
Db url = jdbc:mysql://localhost:3306/test
Db username = cxuan
Db password = 111111
- 可以看到上述代码并没有显示调用printValues 方法,默认是以单元测试的方式进行的。
四、@PropertySource 与 @Import
@Import 可以用来导入 @PropertySource 标注的类,具体代码如下:
- 新建一个PropertySourceReadApplication 类,用于读取配置文件并测试,具体代码如下:
// 导入BasicPropertyWithJavaConfig类
@Import(BasicPropertyWithJavaConfig.class)
public class PropertySourceReadApplication {
@Resource
private Environment env;
@Value("${com.spring.name}")
private String name;
@Bean("context")
public PropertySourceReadApplication contextLoadInitialized(){
// 用environment 读取配置文件
System.out.println(env.getProperty("com.spring.age"));
// 用@Value 读取配置文件
System.out.println("name = " + name);
return null;
}
public static void main(String[] args) {
// AnnotationConnfigApplicationContext 内部会注册Bean
new AnnotationConfigApplicationContext(PropertySourceReadApplication.class);
}
}
- 新建一个BasicPropertyWithJavaConfig 类,用于配置类并加载配置文件
@Configuration
@PropertySource(value = "classpath:application.properties")
public class BasicPropertyWithJavaConfig {
public BasicPropertyWithJavaConfig(){
super();
}
}
启动PropertySourceReadApplication ,console能够发现读取到配置文件中的value值
18
name = cxuan
浅析PropertySource 基本使用-示例
应用实例
以application开头的配置文件,属性和配置文件中的key相同,可直接获取value
@ConfigurationProperties(prefix = "user")
public class UserConfig {
private String name;
private String good;
private String pass;
...get set 方法省略
application-user.yml
user:
name: javaniuniu
pass: 1232342
good: 23esd
javaniuniu 图标banner
" _ _ _ \n" +
" (_) __ ___ ____ _ _ __ (_)_ _ _ __ (_)_ _ \n" +
" | |/ _` \ \ / / _` | '_ \| | | | | '_ \| | | | | \n" +
" | | (_| |\ V / (_| | | | | | |_| | | | | | |_| | \n" +
" _/ |\__,_| \_/ \__,_|_| |_|_|\__,_|_| |_|_|\__,_| \n" +
"|__/============================================== ";
_ _ _
(_) __ ___ ____ _ _ __ (_)_ _ _ __ (_)_ _
| |/ _` \ \ / / _` | '_ \| | | | | '_ \| | | | |
| | (_| |\ V / (_| | | | | | |_| | | | | | |_| |
_/ |\__,_| \_/ \__,_|_| |_|_|\__,_|_| |_|_|\__,_|
|__/==============================================
System.out.println(
" _ _ _ \n" +
" (_) __ ___ ____ _ _ __ (_)_ _ _ __ (_)_ _ \n" +
" | |/ _` \\ \\ / / _` | '_ \\| | | | | '_ \\| | | | | \n" +
" | | (_| |\\ V / (_| | | | | | |_| | | | | | |_| | \n" +
" _/ |\\__,_| \\_/ \\__,_|_| |_|_|\\__,_|_| |_|_|\\__,_| \n" +
"|__/============================================== ");
409. 最长回文串
- 难度:
简单 - 本题涉及算法:
哈希表数组贪心 - 思路:
哈希表检查区域贪心 - 类似题型:
题目 最长回文串
给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写。比如 “Aa” 不能当做一个回文字符串。
示例
输入:"abccccdd"
输出:7
解释:我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
注意:
- 假设字符串的长度不会超过 1010。
解题思路 方法一
- 参考了 拼写单词 构造长度为58的每个元素分别代表一个字母的数组,来简化计算
- 含大小写 长度58,只有大写或小写大小26
- 友情提示:遇到有提示字符串仅包含小写(或者大写)英文字母的题,都可以试着考虑能不能构造长度为26的每个元素分别代表一个字母的数组,来简化计算
代码
public class Solution {
public int longestPalindrome(String s) {
int[] c = new int[58];
for(char cc:s.toCharArray()) {
c[(int)cc-'A']+=1;
}
int res = 0;
boolean flg = false;
for(int i = 0; i<58; i++) {
if(c[i]%2==0&&c[i]!=0){
res+=c[i];
// flg = true;
}
if(c[i]%2==1){
res+=c[i]-1;
flg = true;
}
}
if (flg) {
return res+1;
}else {
return res;
}
}
}
方法二 哈希表
代码
class Solution(object):
def longestPalindrome(self, s):
di = {}
max = 0
for ch in s:
if ch in di:
di[ch] += 1
else:
di[ch] = 1
flag = 0
for d in di:
if di[d]%2==1:
flag = 1
max += di[d]- di[d]%2
else:
max += di[d]
if flag ==1 or len(s)%2==1:
max += 1
else:
return max
return max
方法三:贪心
- 构造长度为58的每个元素分别代表一个字母的数组
代码
public class Solution { public int longestPalindrome(String s) { int[] count = new int[128]; for (char c: s.toCharArray()) count[c]++; int ans = 0; for (int v: count) { ans += v / 2 * 2; if (v % 2 == 1 && ans % 2 == 0) ans++; } return ans; } }
一些高级写法
class Solution:
def longestPalindrome(self, s: str) -> int:
import collections
# 1.统计各字符次数,eg:"ddsad":[3, 1, 1]
count = collections.Counter(s).values()
# 2.统计两两配对的字符总个数,eg: {"ddass":4,"ddsss":4}
x = sum([item//2*2 for item in count if (item//2 > 0)])
# 3.判断是否有没配对的单字符,有结果加一。 eg: {"ddss":4, "ddhjSS":4+1}-->{"ddss":4, "ddhjSS":5}
return x if x == len(s) else x+1
class Solution {
public int longestPalindrome(String s) {
Map<Integer, Integer> count = s.chars().boxed()
.collect(Collectors.toMap(k -> k, v -> 1, Integer::sum));
int ans = count.values().stream().mapToInt(i -> i - (i & 1)).sum();
return ans < s.length() ? ans + 1 : ans;
}
}
错误集
class Solution(object):
def longestPalindrome(self, s):
di = {}
max = 0
for ch in s:
if ch in di:
di[ch] += 1
else:
di[ch] = 1
flag = 0
for d in di:
if di[d]//2> 0: # 忽略了相同字母大于3 输出比预期小1
max += 2 * (di[d]//2)
else:
flag = 1 # 说明有落单的字母
if flag == 1 or len(s)%2==1:
max += 1
else:
return max
return max
class Solution(object):
def longestPalindrome(self, s):
if len(s) <2:
return 1
di = {}
max = 0
for ch in s:
if ch in di:
di[ch] += 1
else:
di[ch] = 1
flag = 0
flag2 = 0
for d in di:
if di[d]//2> 0:
flag = 1
max += 2 * (di[d]//2)
else:
flag2 = 1
if flag ==1 and flag2 == 1 or len(s)%2==1: # 忽略当 s= ab 输出0 预期1
max += 1
else:
return max
return max
class Solution(object):
def longestPalindrome(self, s):
if len(s) <2:
return 1
di = {}
max = 0
for ch in s:
if ch in di:
di[ch] += 1
else:
di[ch] = 1
flag = 0
flag2 = 0
for d in di:
if di[d]//2> 0: # 忽略了 当 s = bbb 4 输出2 预期3
flag = 1
max += 2 * (di[d]//2)
else:
flag2 = 1
if flag ==1 and flag2 == 1:
max += 1
else:
return max
return max
class Solution(object):
def longestPalindrome(self, s):
if len <2:
return 1
di = {}
max = 0
for ch in s:
if ch in di:
di[ch] += 1
else:
di[ch] = 1
flag = 0
flag2 = 0
for d in di:
if di[d]//2> 0:
flag = 1
max += 2 * (di[d]//2)
else:
flag2 = 1
if flag ==1 and flag2 == 1: # 忽略了 当 s=a 时 输出0 预期1
max += 1
else:
return max
return max
836. 矩形重叠
- 难度:
简单 - 本题涉及算法:
- 思路:
检查位置检查区域 - 类似题型:
题目 836. 矩形重叠
矩形以列表 [x1, y1, x2, y2] 的形式表示,其中 (x1, y1) 为左下角的坐标,(x2, y2) 是右上角的坐标。
如果相交的面积为正,则称两矩形重叠。需要明确的是,只在角或边接触的两个矩形不构成重叠。
给出两个矩形,判断它们是否重叠并返回结果
解题思路一 三种情况
-
- rec1[0]>=rec2[2] 不可能相交
-
- rec1[2]<=rec2[0] 不可能相交
-
- x轴相交情况下 在判断 y 轴 y轴也有三种情况 判断方法一样
代码
python
class Solution(object):
def isRectangleOverlap(self, rec1, rec2):
"""
:type rec1: List[int]
:type rec2: List[int]
:rtype: bool
"""
if rec1[0]>=rec2[2] or rec1[2]<=rec2[0]:
return False
else:
if rec1[1]>=rec2[3] or rec1[3]<=rec2[1]:
return False
else:
return True
java
class Solution {
public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
return !(rec1[2] <= rec2[0] || // left
rec1[3] <= rec2[1] || // bottom
rec1[0] >= rec2[2] || // right
rec1[1] >= rec2[3]); // top
}
}
解题思路二 检查区域
- 当
min(rec1[2], rec2[2]) > max(rec1[0], rec2[0])时,这两条线段有交集 - 同理可以得到,当
min(rec1[3], rec2[3]) > max(rec1[1], rec2[1])时,这两条线段有交集class Solution { public boolean isRectangleOverlap(int[] rec1, int[] rec2) { return (Math.min(rec1[2], rec2[2]) > Math.max(rec1[0], rec2[0]) && Math.min(rec1[3], rec2[3]) > Math.max(rec1[1], rec2[1])); } }
解题思路三
矩形重叠要考虑的情况很多,两个矩形的重叠可能有好多种不同的形态。这道题如果用蛮力做的话,很容易遗漏掉某些情况,导致出错。
矩形重叠是二维的问题,所以情况很多,比较复杂。为了简化问题,我们可以考虑将二维问题转化为一维问题。既然题目中的矩形都是平行于坐标轴的,我们将矩形投影到坐标轴上:

矩形投影到坐标轴上,就变成了区间。稍加思考,我们发现:两个互相重叠的矩形,它们在 xx 轴和 yy 轴上投影出的区间也是互相重叠的。这样,我们就将矩形重叠问题转化成了区间重叠问题。
区间重叠是一维的问题,比二维问题简单很多。我们可以穷举出两个区间所有可能的 6 种关系:

可以看到,区间的 6 种关系中,不重叠只有两种情况,判断不重叠更简单。假设两个区间分别是 [s1, e1] 和 [s2, e2] 的话,区间不重叠的两种情况就是 e1 <= s2 和 e2 <= s1。

| 我们就得到区间不重叠的条件:e1 <= s2 | e2 <= s1。将条件取反即为区间重叠的条件。 |
这样,我们就可以写出判断矩形重叠的代码了:
代码
java
public class Solution {
public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
boolean x_overlap = !(rec1[2] <= rec2[0] || rec2[2] <= rec1[0]);
boolean y_overlap = !(rec1[3] <= rec2[1] || rec2[3] <= rec1[1]);
return x_overlap && y_overlap;
// boolean s1 = (rec2[0]-rec1[2])*(rec2[2]-rec1[0])<0;
// boolean s2 = (rec2[1]-rec1[3])*(rec2[3]-rec1[1])<0;
// return s1&&s2;
}
}
339 post articles, 43 pages.