- 难度:
简单 - 本题涉及算法:
小根堆大根堆快排二叉树 - 思路:
小根堆大根堆}快排暴力二叉树数据范围有限时直接计数排序就行了 - 类似题型:
题目 面试题40. 最小的k个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
方法一 暴力
java
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
for (int i=0;i<arr.length-1;i++) {
if (arr[i]>arr[i+1]){
int temp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = temp;
}
for (int j=i;j>0;j--) {
if(arr[j]<arr[j-1]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
int[] res = new int[k];
for (int i = 0;i<k;i++) {
res[i] = arr[i];
}
return res;
}
}
python
class Solution(object):
def getLeastNumbers(self, arr, k):
"""
:type arr: List[int]
:type k: int
:rtype: List[int]
"""
for i in range(len(arr)-1):
if arr[i]> arr[i+1]:
sort(arr,i)
for j in range(i,0,-1):
if arr[j] < arr[j-1]:
lowsort(arr,j)
return arr[:k]
def sort(arr,i):
temp = arr[i]
arr[i] = arr[i+1]
arr[i+1] = temp
return arr
def lowsort(arr,j):
temp = arr[j]
arr[j] = arr[j-1]
arr[j-1] = temp
return arr
方法二 小根堆
/**
* 小根堆
* @param arr
* @param k
* @return
*/
public int[] getLeastNumbersByStack(int[] arr,int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 默认是小根堆,实现大根堆需要重写一下比较器。
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1); // 目的是最大数在第一位
for(int num :arr) {
if(pq.size()<k)
pq.offer(num);
else if(pq.peek()>num) {
pq.poll();
pq.offer(num);
}
}
// 返回堆中的元素
int[] res = new int[pq.size()];
int idx = 0;
for(int num: pq) {
res[idx++] = num;
}
return res;
}
方法三 大根堆
我们用一个大根堆实时维护数组的前 kk 小值。首先将前 kk 个数插入大根堆中,随后从第 k+1k+1 个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可
class Solution:
def getLeastNumbers(self, nums: List[int], k: int) -> List[int]:
if k == 0: return []
n, opposite = len(nums), [-1 * x for x in nums[:k]]
heapq.heapify(opposite)
for i in range(k, len(nums)):
if -opposite[0] > nums[i]:
# 维持堆大小不变
heapq.heappop(opposite)
heapq.heappush(opposite, -nums[i])
return [-x for x in opposite]
方法三 二叉树
/**
* 二叉树
* @param arr
* @param k
* @return
*/
public int[] getLeastNumbersByTree(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// TreeMap的key是数字, value是该数字的个数。
// cnt表示当前map总共存了多少个数字。
TreeMap<Integer, Integer> map = new TreeMap<>();
int cnt = 0;
for (int num: arr) {
// 1. 遍历数组,若当前map中的数字个数小于k,则map中当前数字对应个数+1
if (cnt < k) {
map.put(num, map.getOrDefault(num, 0) + 1);
cnt++;
continue;
}
// 2. 否则,取出map中最大的Key(即最大的数字), 判断当前数字与map中最大数字的大小关系:
// 若当前数字比map中最大的数字还大,就直接忽略;
// 若当前数字比map中最大的数字小,则将当前数字加入map中,并将map中的最大数字的个数-1。
Map.Entry<Integer, Integer> entry = map.lastEntry();
if (entry.getKey() > num) {
map.put(num, map.getOrDefault(num, 0) + 1);
if (entry.getValue() == 1) {
map.pollLastEntry();
} else {
map.put(entry.getKey(), entry.getValue() - 1);
}
}
}
}
方法五 数据范围有限时直接计数排序就行了:O(N)
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 统计每个数字出现的次数
int[] counter = new int[10001];
for (int num: arr) {
counter[num]++;
}
// 根据counter数组从头找出k个数作为返回结果
int[] res = new int[k];
int idx = 0;
for (int num = 0; num < counter.length; num++) {
while (counter[num]-- > 0 && idx < k) {
res[idx++] = num;
}
if (idx == k) {
break;
}
}
return res;
}
}
方法四 排序
# 这个方法很快,总感觉有作弊嫌疑
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
arr.sort()
return arr[:k]
before (2020-04-29更新)
自己的思路
- 给数组排序
用时
08:08-09:09 (1小时)
代码
public class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (arr[0] >= arr[1]) {
int a = arr[1];
arr[1] = arr[0];
arr[0] = a;
}
a:for (int i = 1; i < arr.length - 1; i++) {
if (arr[i] >= arr[i + 1]) {
int c = arr[i + 1];
arr[i + 1] = arr[i];
arr[i] = c;
for (int j = i; j > 0; j--) {
if (arr[j] <= arr[j - 1]) {
int d = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = d;
continue;
}
continue a;
}
}
}
int[] res = new int[k];
for (int q =0;q<k;q++) {
res[q]=arr[q];
}
return res;
}
}
官方解题思路
方法一:排序
思路和算法
对原数组从小到大排序后取出前 kk 个数即可。
class Solution(object):
def getLeastNumbers(self, arr, k):
"""
:type arr: List[int]
:type k: int
:rtype: List[int]
"""
arr.sort()
return arr[:k]
方法二:堆
比较直观的想法是使用堆数据结构来辅助得到最小的 k 个数。堆的性质是每次可以找出最大或最小的元素。我们可以使用一个大小为 k 的最大堆(大顶堆),将数组中的元素依次入堆,当堆的大小超过 k 时,便将多出的元素从堆顶弹出。我们以数组 [5, 4, 1, 3, 6, 2, 9][5,4,1,3,6,2,9], k=3k=3 为例展示元素入堆的过程,如下面动图所示:
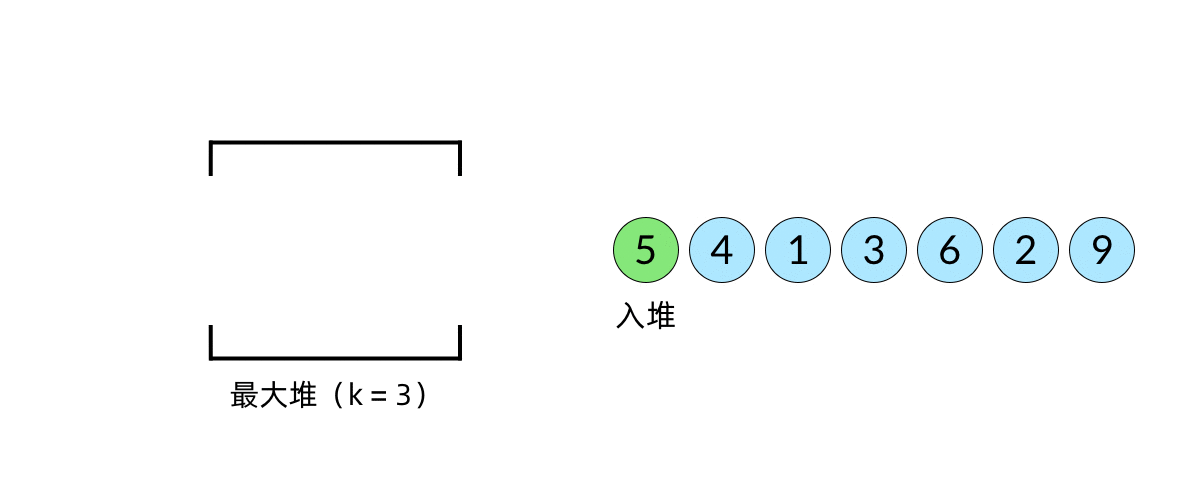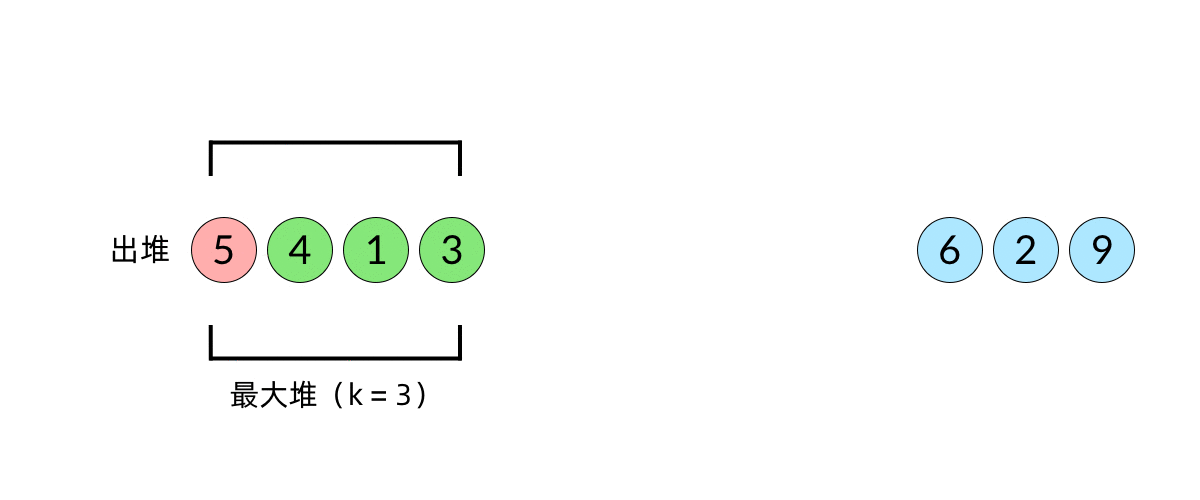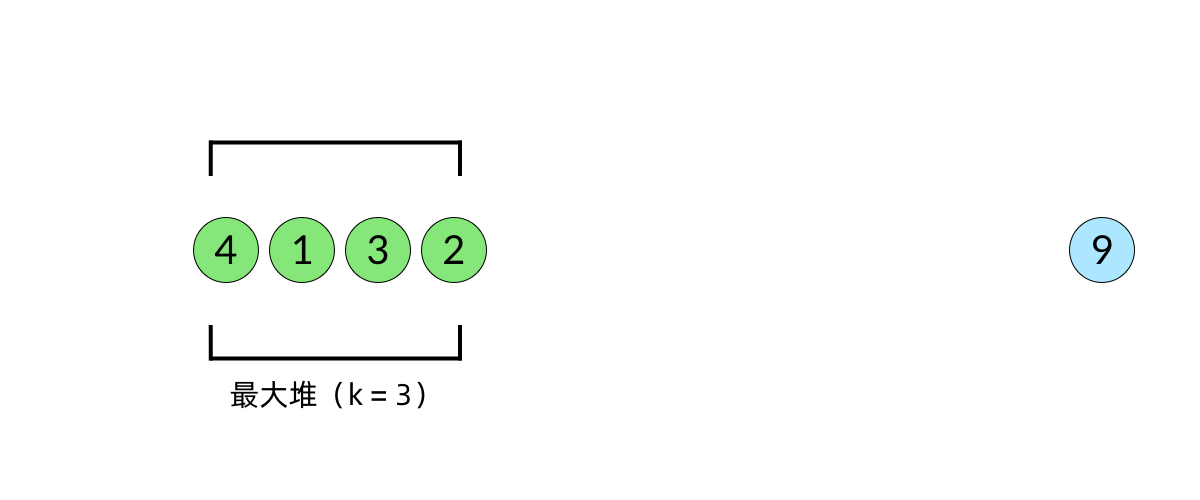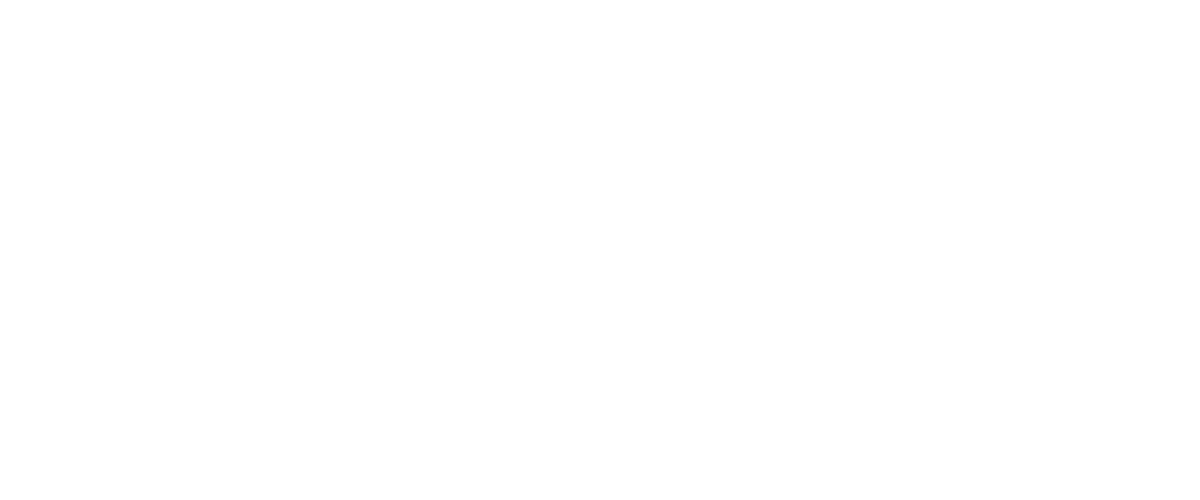
这样,由于每次从堆顶弹出的数都是堆中最大的,最小的 k 个元素一定会留在堆里。这样,把数组中的元素全部入堆之后,堆中剩下的 k 个元素就是最大的 k 个数了。
注意在动画中,我们并没有画出堆的内部结构,因为这部分内容并不重要。我们只需要知道堆每次会弹出最大的元素即可。在写代码的时候,我们使用的也是库函数中的优先队列数据结构,如 Java 中的 PriorityQueue。在面试中,我们不需要实现堆的内部结构,把数据结构使用好,会分析其复杂度即可。
以下是题解代码:
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0) {
return new int[0];
}
// 使用一个最大堆(大顶堆)
// Java 的 PriorityQueue 默认是小顶堆,添加 comparator 参数使其变成最大堆
Queue<Integer> heap = new PriorityQueue<>(k, (i1, i2) -> Integer.compare(i2, i1));
for (int e : arr) {
heap.add(e);
if (heap.size() > k) {
heap.poll(); // 删除堆顶最大元素
}
}
// 将堆中的元素存入数组
int[] res = new int[heap.size()];
int j = 0;
for (int e : heap) {
res[j++] = e;
}
return res;
}
方法三:分治
Top K 问题的另一个分治解法就比较难想到,需要在平时有算法的积累。实际上,“查找第 k 大的元素”是一类算法问题,称为选择问题。找第 k 大的数,或者找前 k 大的数,有一个经典的 quick select(快速选择)算法。这个名字和 quick sort(快速排序)看起来很像,算法的思想也和快速排序类似,都是分治法的思想。
让我们回顾快速排序的思路。快速排序中有一步很重要的操作是 partition(划分),从数组中随机选取一个枢纽元素 v,然后原地移动数组中的元素,使得比 v 小的元素在 v 的左边,比 v 大的元素在 v 的右边,如下图所示:
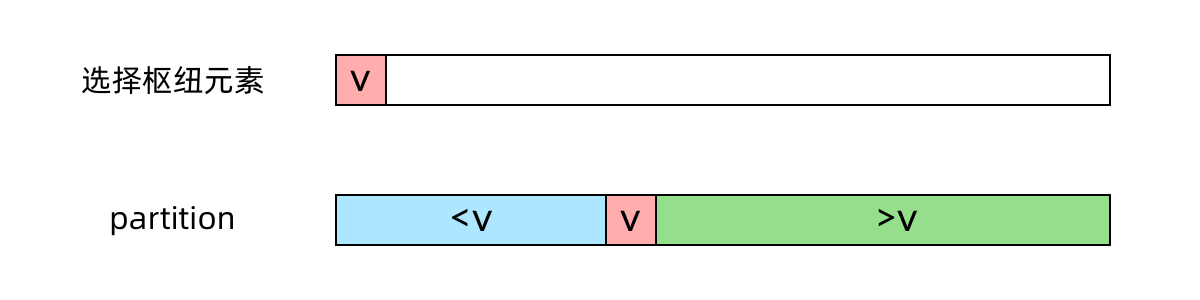
这个 partition 操作是原地进行的,需要 O(n)O(n) 的时间,接下来,快速排序会递归地排序左右两侧的数组。而快速选择(quick select)算法的不同之处在于,接下来只需要递归地选择一侧的数组。快速选择算法想当于一个“不完全”的快速排序,因为我们只需要知道最小的 k 个数是哪些,并不需要知道它们的顺序。
我们的目的是寻找最小的 kk 个数。假设经过一次 partition 操作,枢纽元素位于下标 mm,也就是说,左侧的数组有 mm 个元素,是原数组中最小的 mm 个数。那么:
- 若 k = mk=m,我们就找到了最小的 kk 个数,就是左侧的数组;
- 若 k<mk<m ,则最小的 kk 个数一定都在左侧数组中,我们只需要对左侧数组递归地 parition 即可;
- 若 k>mk>m,则左侧数组中的 mm 个数都属于最小的 kk 个数,我们还需要在右侧数组中寻找最小的 k-mk−m 个数,对右侧数组递归地 partition 即可。 这种方法需要多加领会思想,如果你对快速排序掌握得很好,那么稍加推导应该不难掌握 quick select 的要领。
以下是题解代码:
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0) {
return new int[0];
} else if (arr.length <= k) {
return arr;
}
// 原地不断划分数组
partitionArray(arr, 0, arr.length - 1, k);
// 数组的前 k 个数此时就是最小的 k 个数,将其存入结果
int[] res = new int[k];
for (int i = 0; i < k; i++) {
res[i] = arr[i];
}
return res;
}
void partitionArray(int[] arr, int lo, int hi, int k) {
// 做一次 partition 操作
int m = partition(arr, lo, hi);
// 此时数组前 m 个数,就是最小的 m 个数
if (k == m) {
// 正好找到最小的 k(m) 个数
return;
} else if (k < m) {
// 最小的 k 个数一定在前 m 个数中,递归划分
partitionArray(arr, lo, m-1, k);
} else {
// 在右侧数组中寻找最小的 k-m 个数
partitionArray(arr, m+1, hi, k);
}
}
// partition 函数和快速排序中相同,具体可参考快速排序相关的资料
// 代码参考 Sedgewick 的《算法4》
int partition(int[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
int v = a[lo];
while (true) {
while (a[++i] < v) {
if (i == hi) {
break;
}
}
while (a[--j] > v) {
if (j == lo) {
break;
}
}
if (i >= j) {
break;
}
swap(a, i, j);
}
swap(a, lo, j);
// a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
方法四 快速排序
思路和用快排求第k大的元素类似,在fastSort方法中,我们并不对每一个元素都进行排序,只需要判断一下分区点和k的值的关系 如果k >p+1 说明 分区点左右的都不需要排序了 因为他们的和小于k
class Solution {
public int[] getLeastNumbers(int [] input, int k) {
fastSort(input,0,input.length-1,k);
int[] res = new int[k];
for(int i = 0 ;i< k;i++){
res[i] = input[i];
}
return res;
}
private void fastSort(int[] a,int s,int e,int k){
if(s > e)return;
int p = partation(a,s,e);
if(p+1 == k){
return;
}else if(p+1 < k){
fastSort(a,p+1,e,k);
}else{
fastSort(a,s,p-1,k);
}
}
private int partation(int[] a,int s ,int e){
int privot = a[e];//取最后一个数作为分区点
int i = s;
for(int j = s;j < e;j++){
if(a[j] < privot){
swap(a,i,j);
i++;
}
}
swap(a,i,e);
return i;
}
private void swap(int[] a ,int i ,int j){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
复杂度分析
-
时间复杂度:O(n\log n),其中 n 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂度。
-
空间复杂度:O(\log n),排序所需额外的空间复杂度为 O(\log n)。