5412. 在既定时间做作业的学生人数
- 难度:
简单 - 本题涉及算法:
zip - 思路:
zip - 类似题型:
题目 5412. 在既定时间做作业的学生人数
给你两个整数数组 startTime(开始时间)和 endTime(结束时间),并指定一个整数 queryTime 作为查询时间。
已知,第 i 名学生在 startTime[i] 时开始写作业并于 endTime[i] 时完成作业。
请返回在查询时间 queryTime 时正在做作业的学生人数。形式上,返回能够使 queryTime 处于区间 [startTime[i], endTime[i]](含)的学生人数。
示例 1:
输入:startTime = [1,2,3], endTime = [3,2,7], queryTime = 4
输出:1
解释:一共有 3 名学生。
第一名学生在时间 1 开始写作业,并于时间 3 完成作业,在时间 4 没有处于做作业的状态。
第二名学生在时间 2 开始写作业,并于时间 2 完成作业,在时间 4 没有处于做作业的状态。
第二名学生在时间 3 开始写作业,预计于时间 7 完成作业,这是是唯一一名在时间 4 时正在做作业的学生。
示例 2:
输入:startTime = [4], endTime = [4], queryTime = 4
输出:1
解释:在查询时间只有一名学生在做作业。
示例 3:
输入:startTime = [4], endTime = [4], queryTime = 5
输出:0
示例 4:
输入:startTime = [1,1,1,1], endTime = [1,3,2,4], queryTime = 7
输出:0
示例 5:
输入:startTime = [9,8,7,6,5,4,3,2,1], endTime = [10,10,10,10,10,10,10,10,10], queryTime = 5
输出:5
提示:
startTime.length == endTime.length
1 <= startTime.length <= 100
1 <= startTime[i] <= endTime[i] <= 1000
1 <= queryTime <= 1000
方法一 合并数组
- 使用 zip 合并数组,代码更简洁
class Solution:
def busyStudent(self, startTime: List[int], endTime: List[int], queryTime: int) -> int:
zipped = zip(startTime,endTime)
count = 0
for x,y in zipped:
if queryTime>= x and queryTime <=y:
count += 1
return count
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
5398. 统计二叉树中好节点的数目
- 难度:
中等 - 本题涉及算法:
深度优先搜索 - 思路:
深度优先搜索 - 类似题型:
题目 5398. 统计二叉树中好节点的数目
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
示例 1:
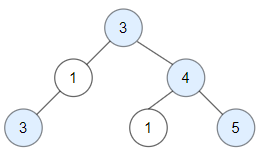
输入:root = [3,1,4,3,null,1,5]
输出:4
解释:图中蓝色节点为好节点。
根节点 (3) 永远是个好节点。
节点 4 -> (3,4) 是路径中的最大值。
节点 5 -> (3,4,5) 是路径中的最大值。
节点 3 -> (3,1,3) 是路径中的最大值。
示例 2:
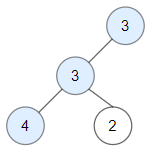
输入:root = [3,3,null,4,2]
输出:3
解释:节点 2 -> (3, 3, 2) 不是好节点,因为 "3" 比它大。
示例 3:
输入:root = [1]
输出:1
解释:根节点是好节点。
提示:
二叉树中节点数目范围是 [1, 10^5] 。
每个节点权值的范围是 [-10^4, 10^4] 。
方法一 深度优先搜索
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def goodNodes(self, root: TreeNode) -> int:
def dfs(root, curr_val):
if not root:return 0 # 终止条件
count = 0
if root.val >= curr_val:
count += 1
curr_val = root.val
count += dfs(root.left,curr_val)
count += dfs(root.right,curr_val)
return count
return dfs(root,- 10 ** 5)
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
5397. 最简分数
- 难度:
中等 - 本题涉及算法:
最大公约数欧几里得法 - 思路:
最大公约数欧几里得法 - 类似题型:
题目 5397. 最简分数
给你一个整数 n ,请你返回所有 0 到 1 之间(不包括 0 和 1)满足分母小于等于 n 的 最简 分数 。分数可以以 任意 顺序返回。
示例 1:
输入:n = 2
输出:["1/2"]
解释:"1/2" 是唯一一个分母小于等于 2 的最简分数。
示例 2:
输入:n = 3
输出:["1/2","1/3","2/3"]
示例 3:
输入:n = 4
输出:["1/2","1/3","1/4","2/3","3/4"]
解释:"2/4" 不是最简分数,因为它可以化简为 "1/2" 。
示例 4:
输入:n = 1
输出:[]
提示:
1 <= n <= 100
欧几里得法(辗转相除法) 通过举例说明1
举例: 105和85的最大公约数
- 第一轮计回算 105÷85=1…20
- 第二轮计算 85÷20=4…5
- 第三轮计算 20÷5=4
- 第三轮没有余数, 因此 105和85的最大公约数就是第三轮计算的被除数 5
欧几里得法(辗转相除法) 通过举例说明2
举例: 21和17的最大公约数
- 第一轮计回算 21÷17=1…4
- 第二轮计算 17÷4=4…1
- 第三轮计算 4÷1=4
- 第三轮没有余数, 因此 105和85的最大公约数就是第三轮计算的被除数 1
方法一 最大公约数
- 解题思路:
- 先求得最大公约数
- 通过最大公约数 是否为 1 来判断 是否为最简分数
- 复杂度分析:
- 时间复杂度 $O(N^2)$
- 空间复杂度 不会算 ,谁帮忙算下 ?
class Solution:
def simplifiedFractions(self, n: int) -> List[str]:
def gcd(a,b):
while b:
a, b = b, a % b
return a
res = []
for i in range(2,n+1):
for j in range(1,i):
if gcd(i,j) == 1:
res.append(str(j) +'/'+str(i))
return res
13. 罗马数字转整数
- 难度:
简单 - 本题涉及算法:
哈希表 - 思路:
哈希表 - 类似题型:
题目 13. 罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
- I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
- X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
- C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。 给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
方法一 哈希表
- 解题思路:
- 把罗马数字用 哈希表 对应保存起来
- 在判断上注意
4, 40, 400, 4000这样的数字
java
class Solution {
public int romanToInt(String s) {
int n = s.length();
if(n == 0) return 0;
char[] arr = s.toCharArray();
Map<Character,Integer> map = new HashMap<>();
map.put('I',1);
map.put('V',5);
map.put('X',10);
map.put('L',50);
map.put('C',100);
map.put('D',500);
map.put('M',1000);
int res = 0;
for(int i = 0; i < arr.length; i++) {
char c = arr[i];
res += map.get(c);
if(i > 0 && map.get(c) > map.get(arr[i-1])) {
res -= 2*map.get(arr[i-1]);
}
}
return res;
}
}
python
class Solution:
def romanToInt(self, s):
"""
:type s: str
:rtype: int
"""
a = {'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000}
ans=0
for i in range(len(s)):
if i<len(s)-1 and a[s[i]]<a[s[i+1]]:
ans-=a[s[i]]
else:
ans+=a[s[i]]
return ans
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
12. 整数转罗马数字
- 难度:
中等 - 本题涉及算法:
- 思路:
这道题告诉又一次告诉我,题解先做出来,不管方法多么的简单 - 类似题型:
题目 12. 整数转罗马数字
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。 给定一个整数,将其转为罗马数字。输入确保在 1 到 3999 的范围内。
示例 1:
输入: 3
输出: "III"
示例 2:
输入: 4
输出: "IV"
示例 3:
输入: 9
输出: "IX"
示例 4:
输入: 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.
示例 5:
输入: 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.
方法一
- 解题思路:
- 把所有的罗马数组列出来 在拼接
python
class Solution: def intToRoman(self, num: int) -> str: thousands = ["", "M", "MM", "MMM"] hundreds = ["", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"] tens = ["", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"] ones = ["", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"] return thousands[num // 1000] + hundreds[num % 1000 // 100] + tens[num % 100 // 10] + ones[num % 10]
- 把所有的罗马数组列出来 在拼接
java
public String intToRoman(int num) {
String[] thousands = new String[]{"", "M", "MM", "MMM"};
String[] hundreds = new String[]{"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
String[] tens = new String[]{"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
String[] ones = new String[]{"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};
return thousands[num / 1000] + hundreds[num % 1000 / 100] + tens[num % 100 / 10] + ones[num % 10];
}
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
8. 字符串转换整数 (atoi)
- 难度:
中等 - 本题涉及算法:
- 思路:
- 类似题型:
题目 8. 字符串转换整数 (atoi)
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。接下来的转化规则如下:
- 如果第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字字符组合起来,形成一个有符号整数。
- 假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成一个整数。
- 该字符串在有效的整数部分之后也可能会存在多余的字符,那么这些字符可以被忽略,它们对函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换,即无法进行有效转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0 。
提示:
- 本题中的空白字符只包括空格字符 ‘ ‘ 。
- 假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
示例 1:
输入: "42"
输出: 42
示例 2:
输入: " -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4:
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
因此无法执行有效的转换。
示例 5:
输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。
方法一
解题思路
- 题目已经给出很详细规则,根据规则可以自己填代码
- 这题的关键在 判断字符是否为数字 ,可以使用下面的代码
Character.isDigit(char ch)
public class Solution {
public int myAtoi(String str) {
char[] chars = str.toCharArray();
int n = chars.length;
int idx = 0;
while (idx < n && chars[idx] == ' ') {
// 去掉前导空格
idx++;
}
if (idx == n) {
//去掉前导空格以后到了末尾了
return 0;
}
boolean negative = false;
if (chars[idx] == '-') {
//遇到负号
negative = true;
idx++;
} else if (chars[idx] == '+') {
// 遇到正号
idx++;
} else if (!Character.isDigit(chars[idx])) {
// 其他符号
return 0;
}
int ans = 0;
while (idx < n && Character.isDigit(chars[idx])) {
int digit = chars[idx] - '0';
if (ans > (Integer.MAX_VALUE - digit) / 10) {
// 本来应该是 ans * 10 + digit > Integer.MAX_VALUE
// 但是 *10 和 + digit 都有可能越界,所有都移动到右边去就可以了。
return negative? Integer.MIN_VALUE : Integer.MAX_VALUE;
}
ans = ans * 10 + digit;
idx++;
}
return negative? -ans : ans;
}
}
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
560. 和为K的子数组
- 难度:
中等 - 本题涉及算法:
前缀和哈希表 - 思路:
前缀和哈希表 - 类似题型:
题目 560. 和为K的子数组
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :
数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ,且整数 k 的范围是 [-1e7, 1e7]。
方法一 前缀和
解题思路
- 题目理解:
- 在数组
nums中找到连续子数组和为k,并返回子数组个数 - 我们假设 从左到右 前缀和为
preSum[0]preSum[0]...preSum[i+1] - 我们再根据下面的 前缀和推倒过程 ,可以得到任意连续子数组和
- 只要 $preSum[right+1] - preSum[left] = k$ 即可得到结果
- 在数组
- 前缀和推倒过程:
preSum[0] = 0 preSum[1] = num[0] = preSum[0] + nums[0] preSum[2] = num[0] + num[1] = preSum[1] + nums[1] preSum[3] = num[0] + num[1] + nums[2] = preSum[2] + nums[2] . . preSum[i+1] = num[0] + num[1] ... + nums[i] = preSum[i] + nums[i] - 复杂度分析:
- 时间复杂度 $O(N^2)$ :假设数组长度为
n,遍历两次 ; - 空间复杂度 $O(N+1)$ :假设数组长度为
n,其中preSum[0]为前缀初始值。
- 时间复杂度 $O(N^2)$ :假设数组长度为
java
class Solution {
public int subarraySum(int[] nums, int k) {
int len = nums.length;
// 计算前缀和数组
int[] preSum = new int[len + 1];
preSum[0] = 0;
for (int i = 0; i < len; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
int count = 0;
for (int left = 0; left < len; left++) {
for (int right = left; right < len; right++) {
// 区间和 [left..right],注意下标偏移
if (preSum[right + 1] - preSum[left] == k) {
count++;
}
}
}
return count;
}
}
python
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
nums_len = len(nums)
pre_sum = [0] * (nums_len+1)
count = 0
for i,num in enumerate(nums):
pre_sum[i+1] = pre_sum[i] + num
for left in range(len(nums)):
for right in range(left,len(nums)):
if pre_sum[right+1] - pre_sum[left] == k:
count += 1
return count
方法二 前缀和 + 哈希表
- 还是前缀和的思想,我们把前缀和放在
map中,map.put(preSum,前缀和出现次数)(数组中可能会有负数,所以可能会重复出现)
java
public int subarraySum(int[] nums, int k) {
int count = 0;
// key:前i个元素的和,value:对应key 出现的个数
Map<Integer,Integer> preSumMap = new HashMap<>();
// 数组下标为 0,则前面数组为空,所以和为 0,且出现一次
preSumMap.put(0, 1);
int preSum = 0;
for(int i = 0;i<nums.length;i++) {
preSum += nums[i];
if (preSumMap.containsKey(preSum-k)){
count += preSumMap.get(preSum-k);
}
preSumMap.put(preSum, preSumMap.getOrDefault(nums[i], 0)+1);
}
return count;
}
python
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
pre_sum = 0
count = 0
pre_sum_dict = collections.defaultdict(int)
pre_sum_dict[0] = 1
for num in nums:
pre_sum += num
if pre_sum - k in pre_sum_dict:
count += pre_sum_dict.get(pre_sum - k)
pre_sum_dict[pre_sum] += 1
return count
- 复杂度分析:
- 时间复杂度 $O(N)$ :假设数组长度为
n,我们遍历数组长度为n - 空间复杂度 $O(N)$ :假设数组长度为
n,哈希表在最坏的情况下,保存n个不同元素
- 时间复杂度 $O(N)$ :假设数组长度为
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
6. Z 字形变换
- 难度:
中等 - 本题涉及算法:
- 思路:
- 类似题型:
6. Z 字形变换
将一个给定字符串根据给定的行数,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 LEETCODEISHIRING 行数为 3 时,排列如下:
L C I R
E T O E S I I G
E D H N
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:”LCIRETOESIIGEDHN”。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入: s = "LEETCODEISHIRING", numRows = 3
输出: "LCIRETOESIIGEDHN
示例 2:
输入: s = "LEETCODEISHIRING", numRows = 4
输出: "LDREOEIIECIHNTSG"
解释:
L D R
E O E I I
E C I H N
T S G
方法一
解题思路
- 题目理解:
- 字符串
s按照Z形状排列字符串,最后按照行打印 - 我们假设
numRows对应的行是 $r_1,r_2…r_n$ , 排序顺序异常是按照 从上到下 $r_1,r_2 …r_n$ 再从下到上 $r_i …r_2,r_1$ ,反复进行 - 因此我们的解题思路是:模拟这个行的变化,在遍历
s的同时,把每个字符串添加到对应的行res[i]
- 字符串
- 算法流程:按照顺序遍历
s;res[i] += c: 把每个字符c填入对应行 $r_i$;i += flag: 更新当前字符c对应的行索引;flag = - flag: 在达到 $Z$ 字形转折点时,执行反向。
- 复杂度分析:
- 时间复杂度 $O(N)$ :遍历一遍字符串
s; - 空间复杂度 $O(N)$ :各行字符串共占用 $O(N)$ 额外空间。
- 时间复杂度 $O(N)$ :遍历一遍字符串
代码
python
class Solution(object):
def convert(self, s, numRows):
"""
:type s: str
:type numRows: int
:rtype: str
"""
if numRows < 2:
return s
res = ['' for _ in range(numRows)]
i, flag = 0, -1
for c in s:
res[i] += c
if i==0 or i == numRows - 1 : flag = -flag
i += flag
return ''.join(res)
java
class Solution {
public String convert(String s, int numRows) {
if (numRows < 2)
return s;
List<StringBuilder> rows = new ArrayList<>();
for (int i = 0; i < numRows; i++)
rows.add(new StringBuilder());
int i = 0, flag = -1;
for(char c:s.toCharArray()){
rows.get(i).append(c);
if (i==0 || i==numRows-1)
flag = -flag;
i += flag;
}
StringBuilder res = new StringBuilder();
for(StringBuilder str :rows)
res.append(str);
return res.toString();
}
}
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
339 post articles, 43 pages.