JAVA 牛牛

Home

2. 两数相加

题目 2. 两数相加

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

方法一 按位相加

  • 主要是对 sum 大于10 需要花点时间处理，其他直接通过 按位相加 即可

复杂度分析

  • 时间复杂度：$O(\max(m, n))$，假设 $m$ 和 $n$ 分别表示 $l1$ 和 $l2$ 的长度，上面的算法最多重复 $\max(m, n)$ 次。
  • 空间复杂度：$O(\max(m, n))$， 新列表的长度最多为 $\max(m,n) + 1$。

上代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode head = new ListNode(0);
        ListNode curr = head;

        // 很妙的两个地方 carry 的设置 和 carry >0 的判断 的判断 🌟🌟🌟🌟🌟
        // 记录和大于10时 +1
        // carry >0 当大于10 则向前进 1
        int carry = 0;
        while (carry > 0 || l1 != null || l2 != null) {
            int sum = carry;
            sum += (l1 != null) ? l1.val : 0;
            sum += (l2 != null) ? l2.val : 0;
            carry = sum / 10;
            curr.next = new ListNode(sum % 10);
            curr = curr.next;
            if (l1 != null) l1 = l1.next;
            if (l2 != null) l2 = l2.next;
        }
        return head.next;
    }

}

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        head = ListNode(0);
        curr = head
        # 很妙的两个地方 carry 的设置 和 carry >0 的判断 🌟🌟🌟🌟🌟
        # 记录和大于10时 +1
        # carry >0 当大于10 则向前进 1
        carry = 0
        while carry > 0 or l1  or l2:
            sum = carry
            sum += l1.val if l1 else 0
            sum += l2.val if l2 else 0
            carry = sum // 10

            curr.next = ListNode(sum % 10)
            curr = curr.next

            if l1 : l1 = l1.next
            if l2 : l2 = l2.next
        return head.next
  • 如果你觉得本文对你有帮助，请点赞👍支持
  • 如果有疑惑或者表达不到位的额地方 ，请在下面👇评论区指出

Read more

  • May 13, 2020
  • 0 views

102. 二叉树的层序遍历

  • 难度：中等
  • 本题涉及算法： DFS BFS
  • 思路： DFS BFS
  • 类似题型:

题目 102. 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：

二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

解题思路

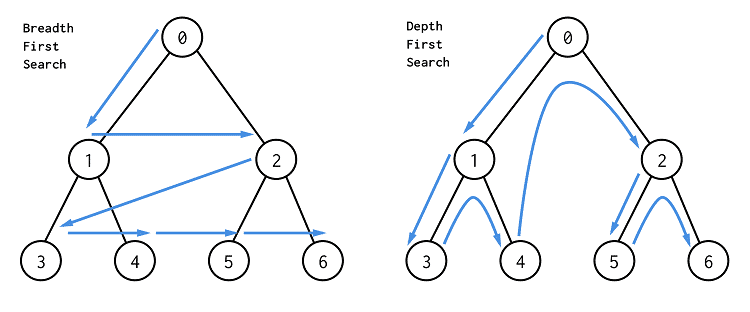
  • 看到二叉树，首选考虑 DFS BFS
  • 如图：左边是BFS，按照层进行搜索；图右边是DFS，先一路走到底，然后再回头搜索

pic1

方法一 BFS

  • BFS 通常和 队列(Queue) 结合使用，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。BFS总共有两个模板：
    1. 如果不需要确定当前遍历到了哪一层，BFS模板如下 
      while queue 不空：
  cur = queue.pop()
  for 节点 in cur的所有相邻节点：
   if 该节点有效且未访问过：
       queue.push(该节点)
    2. 如果要确定当前遍历到了哪一层，BFS模板如下。
      这里增加了level表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。 
      level = 0
while queue 不空：
  size = queue.size()
  while (size --) {
   cur = queue.pop()
   for 节点 in cur的所有相邻节点：
       if 该节点有效且未被访问过：
           queue.push(该节点)
  }
  level ++;

java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        dfs(root,0,res);
        return res;


    }
    private void dfs(TreeNode root,int deepth,List<List<Integer>> res) {
        if (root ==null) return;
        if (deepth==res.size()) res.add(new ArrayList<>());
        res.get(deepth).add(root.val);
        deepth++;
        dfs(root.left,deepth,res);
        dfs(root.right,deepth,res);

    }
}

python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
# BFS
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        queue = collections.deque()
        queue.append(root)
        res = []
        while queue:
            size = len(queue)
            level = []
            for _ in range(size):
                node = queue.popleft()
                if not node:
                    continue
                level.append(node.val)
                queue.append(node.left)
                queue.append(node.right)
            if level: # 如果level 不为空
                res.append(level)
        return res

方法二 DFS

  • DFS 做本题的主要问题是： DFS 不是按照层次遍历的。为了让递归的过程中同一层的节点放到同一个列表中，在递归时要记录每个节点的深度 level。递归到新节点要把该节点放入 level 对应列表的末尾。

  • 当遍历到一个新的深度 level，而最终结果 res 中还没有创建 level 对应的列表时，应该在 res 中新建一个列表用来保存该 level 的所有节点。

java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> curr = new ArrayList<>();
            int size = queue.size();
            for(int i = 0;i<size;i++) {
                TreeNode node =  queue.poll();
                if(node ==null) {
                    continue;
                }
                curr.add(node.val);

                if(node.left!=null){
                    queue.offer(node.left);
                }
                if(node.right!=null){
                    queue.offer(node.right);
                }


                if(i==size-1) {
                    res.add(curr);
                }
            }
        }

        return res;
    }
}

python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
# DFS
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:

        def dfs(root,deepth,res):
            if not root:return # 终止条件
            if deepth==len(res):res.append([])
            res[deepth].append(root.val)
            dfs(root.left,deepth +1,res)
            dfs(root.right,deepth +1,res)
        res = []
        dfs(root,0,res)
        return res

Read more

  • May 13, 2020
  • 0 views

155. 最小栈

  • 难度：简单
  • 本题涉及算法： 前缀和 暴力 哈希表
  • 思路： 前缀和 暴力 哈希表
  • 类似题型:

题目 155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

  • push(x) —— 将元素 x 推入栈中。
  • pop() —— 删除栈顶的元素。
  • top() —— 获取栈顶元素。
  • getMin() —— 检索栈中的最小元素。  

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

pop、top 和 getMin 操作总是在 非空栈 上调用。

方法一 数组

解题思路

  • 我们先用最快捷的方式做题，在慢慢优化代码
  • 使用数组，做数据的增删差操作
  • 而对于获取最小值 使用 Collections.min(list) 获取

java

class MinStack {

    // 数据
    List<Integer> list = null;
    /** initialize your data structure here. */
    public MinStack() {
        list = new ArrayList<>();
    }

    public void push(int x) {
        list.add(x);

    }

    public void pop() {
        list.remove(list.size()-1);

    }

    public int top() {
        return list.get(list.size()-1);

    }

    public int getMin() {
        return Collections.min(list);
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

方法二 辅助栈

解题思路

  • 显然 直接使用 Collections.min(list) 拿到最最小数 会触发隐藏剧情(Collections.min 是怎么实现的)
  • 是的，这里可以用栈，而且用两个，一个是数据栈，一个是辅助栈
  • 数据栈好理解 而辅助栈则是用在 获取最小值中， 通过把最小值放在辅助栈栈顶，来获取最小数据
  • 上代码

java

class MinStack {

    // 数据栈
    private Stack<Integer> data;
    // 辅助栈 用于获取最小值
    private Stack<Integer> helper;
    /** initialize your data structure here. */
    public MinStack() {
        data = new Stack<>();
        helper = new Stack<>();
    }

    public void push(int x) {
        data.add(x);
        if (helper.isEmpty() || helper.peek()>=x)
            helper.add(x);
        else
            helper.add(helper.peek());

    }

    public void pop() {
        if(!data.isEmpty()) {
            data.pop();
            helper.pop();
        }

    }

    public int top() {
        if(!data.isEmpty())
            return data.peek();
        throw new RuntimeException("栈中元素为空，此操作非法");

    }

    public int getMin() {
        if(!data.isEmpty()) {
            return helper.peek();
        }
        throw new RuntimeException("栈中元素为空，此操作非法");

    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

python

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.stack = [] # 数据栈
        self.helper = [] # 辅助栈


    def push(self, x: int) -> None:
        self.stack.append(x)
        if not self.helper or self.helper[-1] >= x:
            self.helper.append(x)
        else:
            self.helper.append(self.helper[-1])


    def pop(self) -> None:
        if self.stack:
            self.helper.pop()
            return self.stack.pop()


    def top(self) -> int:
        if self.stack:
            return self.stack[-1]


    def getMin(self) -> int:
        if self.helper:
            return self.helper[-1]



# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

Read more

  • May 12, 2020
  • 0 views

快速幂

快速幂

计算 $x^ n$ 通常需要 $n$ 次乘法, 时间复杂度为 $O(n)$ , 当 $n$ 非常大的时候, 运算效率很低.

快速幂是通过把 $n$ 转化为二进制来实现的. 例如: 计算 $x^{14}$, 14 可以用二进制表示为:

$14 = (1110)_ 2 = 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 $

那么对应的乘法可以表示为:

$x^{14} = x^{2 ^3} * x^{2^2} * x^{2 ^1} $

转换后乘法运算次数减少, 每次计算 $x^{2^n}$, 再决定是否将这个数字加入到最终结果里面去. 代码如下:

def fpowx(x, n):
    res = 1
    while n:
        if n & 1:
            res = res * x
        # compute x^2 x^4 x^8
        x *= x
        n >>= 1
    return res

乘法防止溢出

注: 对于 python 没有任何帮助, python整数直接相乘取模会快10倍

f_multi: 0.030360s
s_multi: 0.003781s

防止溢出的乘法和快速幂类似, 出现的原因是, 想两个数直接相乘发生溢出时, 改为相加运算, 并且可以直接取模. 这样保证了数据的正确性.

例如 $x\times 14$ 可以转化为:

$x\times 14 = 8\times x + 4\times x + 2\times x$

def fmulti(m, n, mod=10 ** 9 + 7):
    res = 0
    while n:
        if n & 1:
            res += m
        m = (m + m) % mod
        res %= mod
        n >>= 1
    return res

Read more

  • May 12, 2020
  • 0 views

50. Pow(x, n)

  • 难度：中等
  • 本题涉及算法： 递归 折半计算
  • 思路： 递归 折半计算
  • 类似题型:

50. Pow(x, n)

实现 pow(x, n) ，即计算 x 的 n 次幂函数。

示例 1:

输入: 2.00000, 10
输出: 1024.00000

示例 2:

输入: 2.10000, 3
输出: 9.26100

示例 3:

输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25

说明:

-100.0 < x < 100.0
n 是 32 位有符号整数，其数值范围是 [−231, 231 − 1] 。

方法一 暴力

解题思路 时间会超时

  • 先对 n 的正负做判断
  • 当 n 为正数 $x^n$
  • 当 n 为负数 $(1/x)^n$

    java

    class Solution {
  public double myPow(double x, int n) {
      double a = 1.0;
      if(n<0) {
          x = 1/x;
          n = -n;
      }
      for(int i = 0;i<n;i++) {
          a *=x;
      }
      return a;
  }
}

方法二 改良暴力

  • 通过折半计算，每次把 n 减半，降低空间复杂度

    java

    class Solution {
  public double myPow(double x, int n) {
      double a = 1.0;
      if(n<0) {
          x = 1/x;
          n = -n;
      }
      for(int i = n;i != 0;i /= 2) {
          if (i % 2 != 0)
              a *= x;
          x *=x;
      }
      return a;
  }
}

python

class Solution(object):
    def myPow(self, x, n):
        """
        :type x: float
        :type n: int
        :rtype: float
        """
        res = 1;
        if n == 0:
            return 1
        if n < 0:
            x = 1 / x
            n = -n
        while n:
            if n % 2 == 0:
                x *= x
                n /= 2
            else:
                res *=x
                n -= 1
        return res

方法三 递归

解题思路

主要是注意n的正负，这个题比较简单了，直接递归调用就行。

如果 n 是负数，那么相当于求 (1/x)^(-n)。 如果 n 是正数 且 奇数，那么结果需要单独乘以 x 如果 n 是正数 且 偶数，求 (x^2)^(n/2)，一直递归下去即可。 时间复杂度是 $O(1)$，空间复杂度是 $O(1)$。 我认为这个代码是 $O(1)$，因为n只有32位，循环次数是有上限的常数

代码

class Solution {
    public double myPow(double x, int n) {
        if(n==0)
            return 1;
        if(n<0) {
            x = 1/x;
            n = -n;
        }
        if (n%2!=0)
            return x * myPow(x,n-1);
        return myPow(x*x,n/2);
    }
}

python

class Solution(object):
    def myPow(self, x, n):
        """
        :type x: float
        :type n: int
        :rtype: float
        """
        if n == 0:
            return 1
        if n < 0:
            x = 1 / x
            n = -n
        if n % 2:
            return x * self.myPow(x, n - 1)
        return self.myPow(x * x, n / 2)

快速幂

计算 $x^ n$ 通常需要 $n$ 次乘法, 时间复杂度为 $O(n)$ , 当 $n$ 非常大的时候, 运算效率很低.

快速幂是通过把 $n$ 转化为二进制来实现的. 例如: 计算 $x^{14}$, 14 可以用二进制表示为:

$14 = (1110)_ 2 = 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 $

那么对应的乘法可以表示为:

$x^{14} = x^{2 ^3} * x^{2^2} * x^{2 ^1} $

转换后乘法运算次数减少, 每次计算 $x^{2^n}$, 再决定是否将这个数字加入到最终结果里面去. 代码如下:

python

class Solution:
    def myPow(self, x: float, n: int) -> float:
        res = 1
        if n < 0:
            n = -n
            x = 1/x
        while n:
            if n & 1:
                res *= x
            x *= x
            n = n >> 1
        return res

java

class Solution {
    public double myPow(double x, int n) {
        double res = 1.0;
        long b = n; // 防止 int 溢出， 使用 long
        if(b<0) {
            x = 1/x;
            b = -b;
        }
        while (b >0) {
            if ((b&1) ==1)
                res *= x;
            x *= x;
            b >>= 1;
        }
        return res;
    }
}

Read more

  • May 11, 2020
  • 0 views

1248. 统计「优美子数组」

  • 难度：中等
  • 本题涉及算法： 滑动窗口 按位与运算
  • 思路： 滑动窗口 按位与运算
  • 类似题型:

题目 1248. 统计「优美子数组」

给你一个整数数组 nums 和一个整数 k。

如果某个 连续 子数组中恰好有 k 个奇数数字，我们就认为这个子数组是 「优美子数组」。

请返回这个数组中「优美子数组」的数目。

示例 1：

输入：nums = [1,1,2,1,1], k = 3
输出：2
解释：包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。

示例 2：

输入：nums = [2,4,6], k = 1
输出：0
解释：数列中不包含任何奇数，所以不存在优美子数组。

示例 3：

输入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出：16

 

提示：

1 <= nums.length <= 50000
1 <= nums[i] <= 10^5
1 <= k <= nums.length

方法一 滑动窗口

  1. 不断右移 right 指针来扩大滑动窗口，使其包含 k 个奇数；

  2. 若当前滑动窗口包含了 k 个奇数，则如下「计算当前窗口的优美子数组个数」：

    • 统计第 1 个奇数左边的偶数个数 leftEvenCnt。 这 leftEvenCnt 个偶数都可以作为「优美子数组」的起点，因此起点的选择有 leftEvenCnt + 1 种（因为可以一个偶数都不取，因此别忘了 +1 喔）。
    • 统计第 k 个奇数右边的偶数个数 rightEvenCnt 。 这 rightEvenCnt 个偶数都可以作为「优美子数组」的终点，因此终点的选择有 rightEvenCnt + 1 种（因为可以一个偶数都不取，因此别忘了 +1 喔）。
    • 因此「优美子数组」左右起点的选择组合数为 (leftEvenCnt + 1) * (rightEvenCnt + 1)。
  • 判断奇偶数 
    if ((nums[i] & 1) ==1) {
// 基数
}
if ((nums[i] & 1) ==1) {
// 偶数
}

class Solution {
    public int numberOfSubarrays(int[] nums, int k) {
        int left = 0, right = 0, oddCnt = 0, res = 0;
        while (right < nums.length) {
            // 右指针先走，每遇到一个奇数则 oddCnt++。
            if ((nums[right++] & 1) == 1) {
                oddCnt++;
            }

            //  若当前滑动窗口 [left, right) 中有 k 个奇数了，进入此分支统计当前滑动窗口中的优美子数组个数。
            if (oddCnt == k) {
                // 先将滑动窗口的右边界向右拓展，直到遇到下一个奇数（或出界）
                // rightEvenCnt 即为第 k 个奇数右边的偶数的个数
                int tmp = right;
                while (right < nums.length && (nums[right] & 1) == 0) {
                    right++;
                }
                int rightEvenCnt = right - tmp;
                // leftEvenCnt 即为第 1 个奇数左边的偶数的个数
                int leftEvenCnt = 0;
                while ((nums[left] & 1) == 0) {
                    leftEvenCnt++;
                    left++;
                }
                // 第 1 个奇数左边的 leftEvenCnt 个偶数都可以作为优美子数组的起点
                // (因为第1个奇数左边可以1个偶数都不取，所以起点的选择有 leftEvenCnt + 1 种）
                // 第 k 个奇数右边的 rightEvenCnt 个偶数都可以作为优美子数组的终点
                // (因为第k个奇数右边可以1个偶数都不取，所以终点的选择有 rightEvenCnt + 1 种）
                // 所以该滑动窗口中，优美子数组左右起点的选择组合数为 (leftEvenCnt + 1) * (rightEvenCnt + 1)
                res += (leftEvenCnt + 1) * (rightEvenCnt + 1);

                // 此时 left 指向的是第 1 个奇数，因为该区间已经统计完了，因此 left 右移一位，oddCnt--
                left++;
                oddCnt--; // 这一步很关键 决定了执行下一个区间
            }

        }

        return res;
    }
}

Read more

  • May 11, 2020
  • 0 views

1. 两数之和

题目 1. 两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

方法一 暴力

java

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2];
        for(int i=0;i<nums.length;i++) {
            for(int j=i+1;j<nums.length;j++) {
                if((nums[i]+nums[j])==target) {
                    res[0] = i;
                    res[1] = j;
                    break;
                }
            }
        }
        return res;
    }
}

方法二 前缀和 哈希表

解题思路

  • 这道题本身如果通过暴力遍历的话也是很容易解决的，时间复杂度在 $O(n^2)$
  • 由于哈希查找的时间复杂度为 $O(1)$，所以可以利用哈希容器 map 降低时间复杂度
  • 遍历数组 nums，i 为当前下标，每个值都判断map中是否存在 target-nums[i] 的 key 值
  • 如果存在则找到了两个值，如果不存在则将当前的 (nums[i],i) 存入 map 中，继续遍历直到找到为止
  • 如果最终都没有结果则抛出异常
  • 时间复杂度：$O(n)$

java

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        int[] res = new int[2];
        for(int i =0;i<nums.length;i++) {
            if(map.containsKey(target - nums[i])) {
                res[0] = map.get(target - nums[i]);
                res[1] = i;
                return res;
            }
            map.put(nums[i],i);
        }
        return null;
    }
}

python

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        res = []
        nums_dict = {}
        for i, num in enumerate(nums):
            if target - num in nums_dict:
                res.append(nums_dict.get(target - num))
                res.append(i)
                return res
            nums_dict[num] = i

Read more

  • May 11, 2020
  • 0 views
Search