JAVA 牛牛

排序

  • Apr 21, 2020
  • 0 views

选择排序

思路

每一轮选取未排定的部分中最小的部分交换到未排定部分的最开头，经过若干个步骤，就能排定整个数组。即：先选出最小的，再选出第 2 小的，以此类推。

参考代码

import java.util.Arrays;

public class Solution {

    // 选择排序：每一轮选择最小元素交换到未排定部分的开头

    public int[] sortArray(int[] nums) {
        int len = nums.length;
        // 循环不变量：[0, i) 有序，且该区间里所有元素就是最终排定的样子
        for (int i = 0; i < len - 1; i++) {
            // 选择区间 [i, len - 1] 里最小的元素的索引，交换到下标 i
            int minIndex = i;
            for (int j = i + 1; j < len; j++) {
                if (nums[j] < nums[minIndex]) {
                    minIndex = j;
                }
            }
            swap(nums, i, minIndex);
        }
        return nums;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }

    public static void main(String[] args) {
        int[] nums = {5, 2, 3, 1};
        Solution solution = new Solution();
        int[] res = solution.sortArray(nums);
        System.out.println(Arrays.toString(res));
    }
}

总结：

  • 算法思想 1：贪心算法：每一次决策只看当前，当前最优，则全局最优。注意：这种思想不是任何时候都适用。

  • 算法思想 2：减治思想：外层循环每一次都能排定一个元素，问题的规模逐渐减少，直到全部解决，即「大而化小，小而化了」。运用「减治思想」很典型的算法就是大名鼎鼎的「二分查找」。

  • 优点：交换次数最少。

「选择排序」看起来好像最没有用，但是如果在交换成本较高的排序任务中，就可以使用「选择排序」（《算法 4》相关章节课后练习题）。

依然是建议大家不要对算法带有个人色彩，在面试回答问题的时候和看待一个人和事物的时候，可以参考的回答模式是「具体问题具体分析，在什么什么情况下，用什么什么算法」。

复杂度分析：

时间复杂度：O(N^2)，这里 NN 是数组的长度；
空间复杂度：O(1)，使用到常数个临时变量。

插入排序（熟悉）

思路

思路：每次将一个数字插入一个有序的数组里，成为一个长度更长的有序数组，有限次操作以后，数组整体有序。

pic1

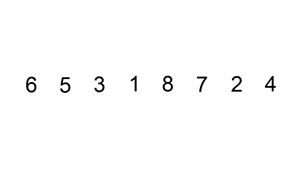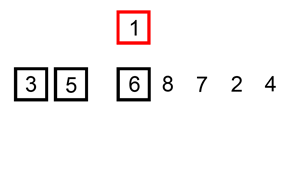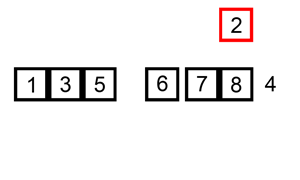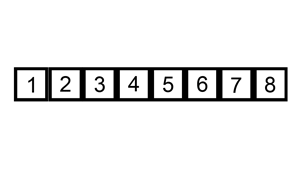
参考代码

public class Solution {

    // 插入排序：稳定排序，在接近有序的情况下，表现优异

    public int[] sortArray(int[] nums) {
        int len = nums.length;
        // 循环不变量：将 nums[i] 插入到区间 [0, i) 使之成为有序数组
        for (int i = 1; i < len; i++) {
            // 先暂存这个元素，然后之前元素逐个后移，留出空位
            int temp = nums[i];
            int j = i;
            // 注意边界 j > 0
            while (j > 0 && nums[j - 1] > temp) {
                nums[j] = nums[j - 1];
                j--;
            }
            nums[j] = temp;
        }
        return nums;
    }
}

优化：

  • 「将一个数字插入一个有序的数组」这一步，可以不使用逐步交换，使用先赋值给「临时变量」，然后「适当的元素」后移，空出一个位置，最后把「临时变量」赋值给这个空位的策略（就是上面那张图的意思）。编码的时候如果不小心，可能会把数组的值修改，建议多调试；

  • 特点：「插入排序」可以提前终止内层循环（体现在 nums[j - 1] > temp 不满足时），在数组「几乎有序」的前提下，「插入排序」的时间复杂度可以达到 O(N)O(N)；

  • 由于「插入排序」在「几乎有序」的数组上表现良好，特别地，在「短数组」上的表现也很好。因为「短数组」的特点是：每个元素离它最终排定的位置都不会太远。为此，在小区间内执行排序任务的时候，可以转向使用「插入排序」。

复杂度分析：

  • 时间复杂度：O(N^2)，这里 NN 是数组的长度；
  • 空间复杂度：O(1)，使用到常数个临时变量。
Search