JAVA 牛牛

二分查找

  • Apr 22, 2020
  • 0 views

通用解题模板：

区间定义：[l, r) 左闭右开

  • f(m)函数 满足该条件，可直接返回对应位置
  • g(m)函数 满足该条件，可移动右边界
  • 同理，在else中移动左边界
  • 如果没有这个条件的判断就是 lowwer_bound和higher_bound. 
    def binary_search(l, r):
  while l < r:
      m = l + (r - l) // 2
      if f(m):    # 判断找了没有，optional
          return m
      if g(m):
          r = m   # new range [l, m)
      else:
          l = m + 1 # new range [m+1, r)
  return l    # or not found

lower bound: find index of i, such that A[i] >= x

def lowwer_bound(self, nums, target):
    # find in range [left, right)
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right - left) / 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left

upper bound: find index of i, such that A[i] > x

def higher_bound(self, nums, target):
    # find in range [left, right)
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right - left) / 2
        if nums[mid] <= target:
            left = mid + 1
        else:
            right = mid
    return left

只要符合单调，就可以二分

题目1 面试题56 - I. 数组中数字出现的次数

一个整型数组 `nums` 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是`O(n)`，空间复杂度是`O(1)`。

如果我们对所有的数字进行异或，假设只出现一次的数字分别是 p 和 q，那么最终的结果 p⊕q，此时我们不知道 p 和 q 分别是什么。但是如果我们能把 p 和 q 从 数组里面区分开来呢？假设我们知道了某个数 r，r 是介于 p 和 q 之间，那么我们可以把整个数组分成两部分 —— a<=r或 a>r 。并且，一个数组里有 p，另一个数组里有 q。那么对这两部分的数字分别求异或和，结果就变成了 p 和 q 。完美！这样就把问题转换成了我们已经解决的问题上了！

在某次消防演习中，消防员问一程序员如果公司着火要怎么办，程序员回答使用灭火器灭火。消防员再问，如果没有着火怎么办？程序员回答把公司点着，这样就把问题归结到一个已经解决的问题上了！手动划掉

我举个栗子来说一下上面的想法：
我们看下数组 [1,2,10,4,1,4,3,3]，我们知道 p 和 q 是 2 和 10。 中间的数字我们假设是 3，根据 a<=3 和 a>3 划分成了[1,2,1,3,3] 和 [10,4,4]。这两个数组分别异或就是 2 和 10。

但是还没有解决，怎么找到 pp 和 qq 中间的数字 rr 呢？

二分！！！

为什么是 二分 呢？一个暴力的方法就是从数组最小的元素到最大的元素枚举所有可能的 r，然后根据 a<=r和 a>r 化成两个数组，再看两个数组的异或和是不是都不为 0，如果是，那我们就找到了 r。但是注意到，在枚举 r 的时候，两个数组的异或和是否为0这个性质是单调的！

下图是从数组最小的元素到最大的元素枚举 rr 的过程。

为了更能体现出来单调的性质，我把 r=0 和 r=11 也加进来了。

pic1

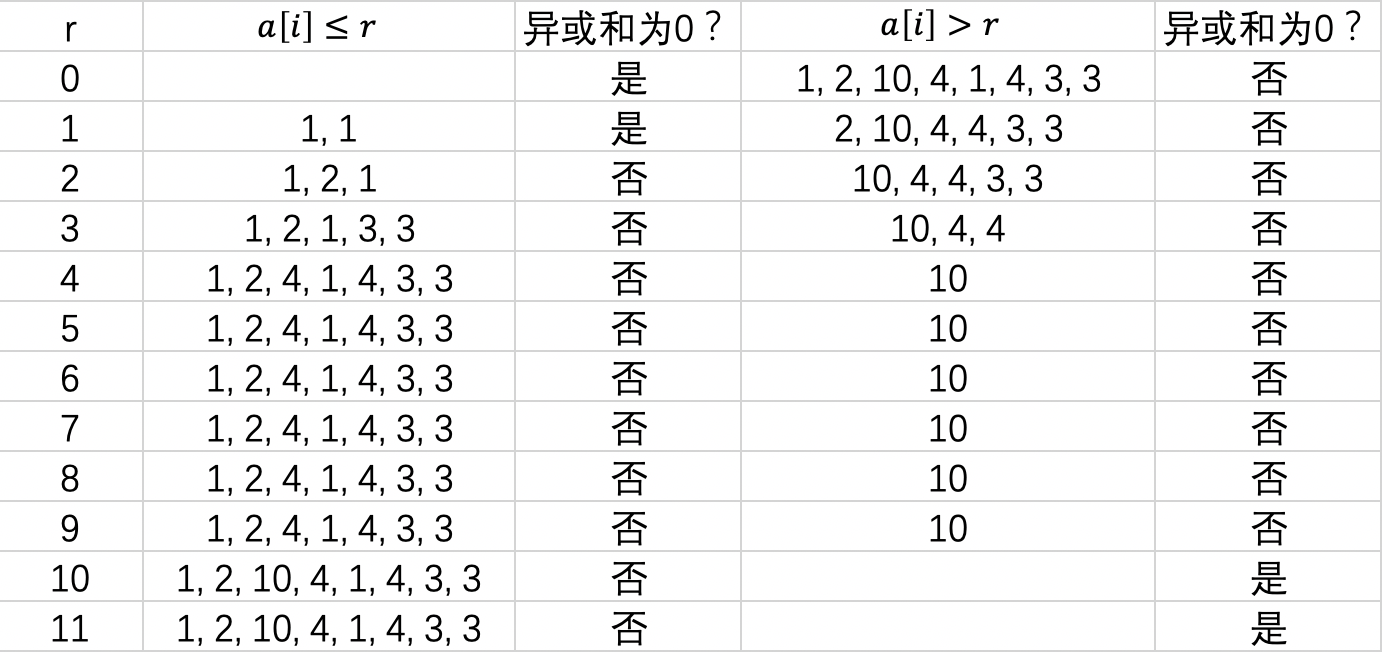
简单来说，

  • 如果当前左边的数组异或和为 00, 右边不为 00，说明当前枚举的 rr 小了；
  • 如果当前左边的数组异或和不为 00, 右边也不为 00，说明当前枚举的 rr 是符合要求的，左右数组异或的结果就是答案；
  • 如果当前左边的数组异或和不为 00, 右边为 00，说明当前枚举的 rr 大了；
  • 这就是单调的样子。所以可以二分。

记住，只要符合单调，就可以二分！！！

但是，你以为这完了吗？异或和为 0 其实并不代表 要找的元素不在这里面，因为有可能 00 只出现了 11 次！ 所以这种思路需要特判一下某个数为 00 的情况。

class Solution {
    public int[] singleNumbers(int[] nums) {
        int sum = 0, min = Integer.MAX_VALUE, max = Integer.MIN_VALUE, zeroCount = 0;
        for (int num : nums) {
            if (num == 0) {
                zeroCount += 1;
            }
            min = Math.min(min, num);
            max = Math.max(max, num);
            sum ^= num;
        }
        // 需要特判一下某个数是0的情况。
        if (zeroCount == 1) {
            return new int[]{sum, 0};
        }
        int lo = min, hi = max;
        while (lo <= hi) {
            // 根据 lo 的正负性来判断二分位置怎么写，防止越界。
            int mid = lo < 0 ? lo + hi >> 1 : lo + (hi - lo) / 2;
            int loSum = 0, hiSum = 0;
            for (int num : nums) {
                if (num <= mid) {
                    loSum ^= num;
                } else {
                    hiSum ^= num;
                }
            }
            if (loSum != 0 && hiSum != 0) {
                // 两个都不为0，说明 p 和 q 分别落到2个数组里了。
                return new int[]{loSum, hiSum};
            }
            if (loSum == 0) {
                // 说明 p 和 q 都比 mid 大，所以比 mid 小的数的异或和变为0了。
                lo = mid;
            } else {
                // 说明 p 和 q 都不超过 mid
                hi = mid;
            }
        }
        // 其实如果输入是符合要求的，程序不会执行到这里，为了防止compile error加一下
        return null;
    }
}

二分查找相关题目

参考视频

Search