类似题型

• 152. 乘积最大子数组
• 53. 最大子序和
• 198. 打家劫舍
• 213. 打家劫舍 II

文案

动态规范总体思想

1. 基于 斐波那契数列

1. 动态规划解决来递归的重复子问题，递归空间时间复杂度 $O(n^2)$ ,动态规划 $O(n)$
   • 比如说 下面的 例题二 中通过数组保存过程状态，需要用的时候直接获取到，不需要在算一遍

做题思路

• 寻找子问题
• 选择第 i 个数字
• 不选 第 i 个数字
• 找出口

例题一

在数组中找出数字和最大的数，其中两个数不能是相邻的两个数

示例

arr = [1,2,4,1,7,8,3]
返回最大数为 15 [1,4,8]

方法一 动态规划

解题思路

• 如图 思路分析
  1. 先为数组添加下标 方便理解
  2. 根据条件可知 只能找不相邻的两个数
  3. 假设 opt[i] 表示到下标为 i 的最佳方案
  4. 选择下标为 i 的方案 opt[i-2] + arr[i]
  5. 不选择下标为 i 的方案 opt[i-1]
  6. 再比较 这两个的大小
  7. 找出口
     • 当数组 arr 只有一个数字的时候 最大数 opt[0] = arr[0]
     • 当数组 arr 有两个数字的时候 最大数 opt[1] = max(arr[0],arr[1])
• 根据思路可推到出公式

动态规划写法

python

class Solution:
    def massage(self, nums: List[int]) -> int:
        lenNums = len(nums)
        if nums == None or lenNums ==0:
            return 0
        opt = [0] * lenNums
        if lenNums == 1:
            return nums[0]
        if lenNums == 2:
            return max(nums[0],nums[1])
        opt[0] = nums[0]
        opt[1] = max(nums[0],nums[1])
        for i in range(2,lenNums):
            a = opt[i-2] + nums[i]
            b = opt[i-1]
            opt[i] = max(a,b)
        return opt[lenNums-1]

java

public class Solution {

    public int massage(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        if (len == 1) {
            return nums[0];
        }
        int[] opt = new int[len];
        opt[0] = nums[0];
        opt[1] = Math.max(nums[0],nums[1]);
        for(int i = 2;i<len;i++) {
            int a = opt[i-2] + nums[i];
            int b = opt[i-1];
            opt[i] = Math.max(a,b);
        }
        return opt[len-1];
    }
}

递归写法

• 需要把 arr 传递进去

  def rec_opt(arr,i):
    # 找出口
    if i ==0:
        return arr[0]
    elif i==1:
        return max(arr[0],arr[1])
    else:
        a = rec_opt(arr,i-2) + arr[i] #选择arr[i]
        b = rec_opt(arr,i-1)# 不选arr[i]
        return max(a,b)
  

例题二

在数组中找出和为s的数，有则返回 True，没有则返回 False

示例

arr = [3,34,4,12,5,2]
k = 9
结果 为True (4+5=9)

方法一 动态规划

解题思路

• 如图 思路分析
  1. 先为数组添加下标 方便理解
  2. 根据条件可知 需要找出和为 s 的数
  3. 我们假设 subset(i,s) i 表示数组下标 s 表示需要求的数
  4. opt[i] 表示到下标为 i 的最佳方案
  5. 选择下标为 i 的方案 那么剩下的数组需要 subset(arr[i-1],s-arr[i])
  6. 不选择下标为 i 的方案 那么剩下的数组需要 subset[i-1] + arr[i]
  7. 在比较 这两个的大小
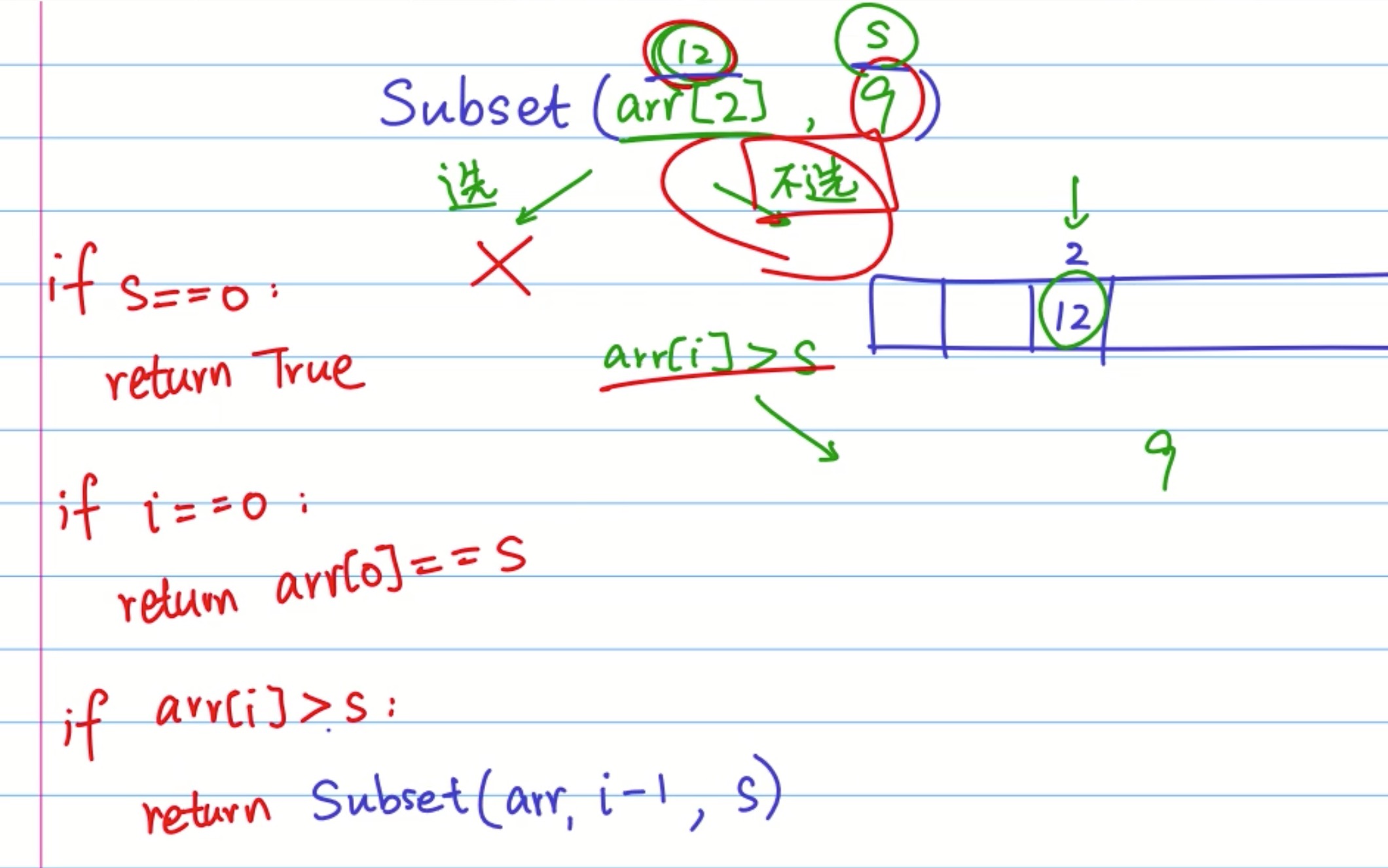
  8. 找出口
     • 当 s = 0 表示 i 之前的数字加起来已经等于 s 了 则直接返回 True
     • 当 i = 0 的时候，表示 arr[0] == s 才能返回为 True
     • 当左边的数字比右边的 s 还有大，则(s-arr[i]<0) ,所以只能选择第二种情况，subset[i-1] + arr[i]
• 根据思路可推到出公式

动态规划写法

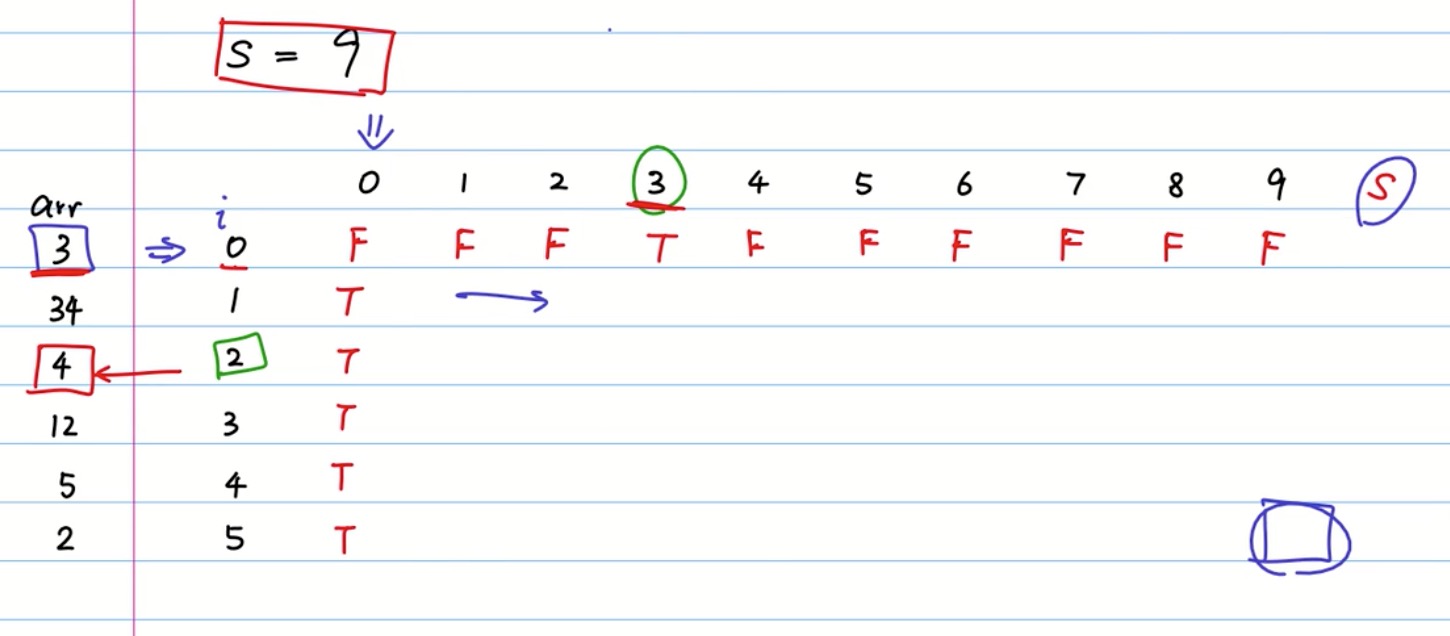
• 需要使用二维数组来保存中间所有的动态过程
• 通常使用二维数组 ，都会把二维数组的下标分别加 1
• 返回 二维数组的最后一个数组

  import numpy as np
  def dp_subset(arr,S):
    subset = np.zeros((len(arr),S+1),dtype = bool)
    subset[:,0] = True
    subset[0,:] = False
    subset[0,arr[0]] = True
    for i in range(1,len(arr)):
        for s in range(1,S+1):
            if arr[i]>s:
                subset[i,s] = subset[i-1,s]
            else:
                a = subset[i-1,s-arr[i]] #选择arr[i]
                b = subset[i-1,s] # 不选arr[i]
                subset[i,s] = a or b
    r ,c = subset.shape
    return subset[r-1,c-1]
  

递归写法

• 需要把 arr 传递进去

  arr = [3,34,4,12,5,2]
  # 递归写法
  def rec_subset(arr,i,s):
    # 找出口
    if s ==0:
        return True
    if i ==0:
        return arr[0]==s
    if arr[i]>s:
        return rec_subset(arr,i-1,s)
    else:
        a = rec_subset(arr,i-1,s-arr[i]) #选择arr[i]
        b = rec_subset(arr,i-1,s) # 不选arr[i]
        return a or b
  

参考视频

• 动态规划 (第1讲)
• 动态规划 (第2讲)