100. 相同的树
- 难度:
简单 - 本题涉及算法:
递归 - 思路:
递归 - 类似题型:
题目 100. 相同的树
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true
示例 2:
输入: 1 1
/ \
2 2
[1,2], [1,null,2]
输出: false
示例 3:
输入: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
输出: false
方法一 递归
python
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
# p and q are both None
if not p and not q:
return True
# one of p and q is None
if not q or not p:
return False
if p.val != q.val:
return False
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
java
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p==null && q == null)
return true;
if (p==null || q == null)
return false;
if (p.val !=q.val)
return false;
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}
参考链接
二叉树算法框架
设计的总路线:
明确一个节点要做的事情,然后剩下的事抛给框架。
void traverse(TreeNode root) {
// root 需要做什么?在这做。
// 其他的不用 root 操心,抛给框架
traverse(root.left);
traverse(root.right);
}
举两个简单的例子体会一下这个思路,热热身。
1. 如何把二叉树所有的节点中的值加一?
void plusOne(TreeNode root) {
if (root == null) return;
root.val += 1;
plusOne(root.left);
plusOne(root.right);
}
2. 如何判断两棵二叉树是否完全相同?
boolean isSameTree(TreeNode root1, TreeNode root2) {
// 都为空的话,显然相同
if (root1 == null && root2 == null) return true;
// 一个为空,一个非空,显然不同
if (root1 == null || root2 == null) return false;
// 两个都非空,但 val 不一样也不行
if (root1.val != root2.val) return false;
// root1 和 root2 该比的都比完了
return isSameTree(root1.left, root2.left)
&& isSameTree(root1.right, root2.right);
}
借助框架,上面这两个例子不难理解吧?如果可以理解,那么所有二叉树算法你都能解决。
二叉搜索树( Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。
如下就是一个符合定义的 BST:
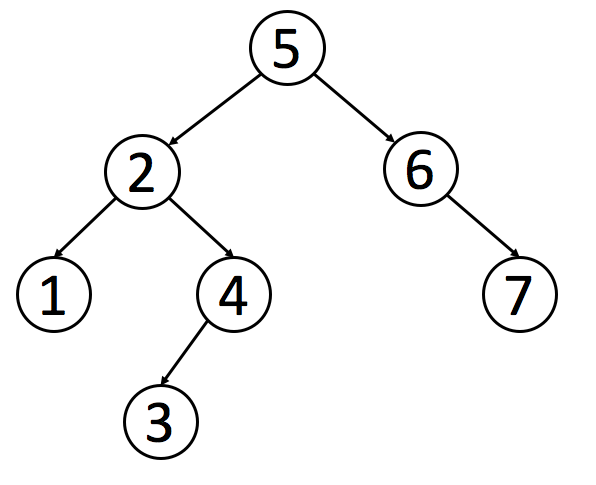
下面实现 BST 的基础操作:判断 BST 的合法性、增、删、查。其中“删”和“判断合法性”略微复杂。
零、判断 BST 的合法性
这里是有坑的哦,我们按照刚才的思路,每个节点自己要做的事不就是比较自己和左右孩子吗?看起来应该这样写代码:
boolean isValidBST(TreeNode root) {
if (root == null) return true;
if (root.left != null && root.val <= root.left.val) return false;
if (root.right != null && root.val >= root.right.val) return false;
return isValidBST(root.left)
&& isValidBST(root.right);
}
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的所有节点,下面这个二叉树显然不是 BST,但是我们的算法会把它判定为 BST。
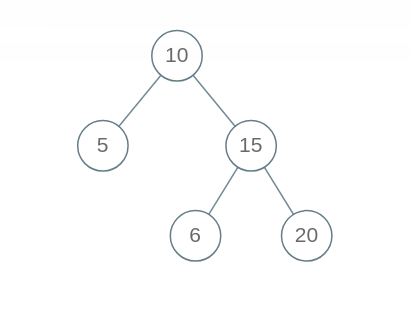
出现错误,不要慌张,框架没有错,一定是某个细节问题没注意到。我们重新看一下 BST 的定义,root 需要做的不只是和左右子节点比较,而是要整个左子树和右子树所有节点比较。怎么办,鞭长莫及啊!
这种情况,我们可以使用辅助函数,增加函数参数列表,在参数中携带额外信息,请看正确的代码:
boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
if (root == null) return true;
if (min != null && root.val <= min.val) return false;
if (max != null && root.val >= max.val) return false;
return isValidBST(root.left, min, root)
&& isValidBST(root.right, root, max);
}
一、在 BST 中查找一个数是否存在
根据我们的指导思想,可以这样写代码:
boolean isInBST(TreeNode root, int target) {
if (root == null) return false;
if (root.val == target) return true;
return isInBST(root.left, target)
|| isInBST(root.right, target);
}
这样写完全正确,充分证明了你的框架性思维已经养成。现在你可以考虑一点细节问题了:如何充分利用信息,把 BST 这个“左小右大”的特性用上?
很简单,其实不需要递归地搜索两边,类似二分查找思想,根据 target 和 root.val 的大小比较,就能排除一边。我们把上面的思路稍稍改动:
boolean isInBST(TreeNode root, int target) {
if (root == null) return false;
if (root.val == target)
return true;
if (root.val < target)
return isInBST(root.right, target);
if (root.val > target)
return isInBST(root.left, target);
// root 该做的事做完了,顺带把框架也完成了,妙
}
于是,我们对原始框架进行改造,抽象出一套针对 BST 的遍历框架:
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
二、在 BST 中插入一个数
对数据结构的操作无非遍历 + 访问,遍历就是“找”,访问就是“改”。具体到这个问题,插入一个数,就是先找到插入位置,然后进行插入操作。
上一个问题,我们总结了 BST 中的遍历框架,就是“找”的问题。直接套框架,加上“改”的操作即可。一旦涉及“改”,函数就要返回 TreeNode 类型,并且对递归调用的返回值进行接收。
TreeNode insertIntoBST(TreeNode root, int val) {
// 找到空位置插入新节点
if (root == null) return new TreeNode(val);
// if (root.val == val)
// BST 中一般不会插入已存在元素
if (root.val < val)
root.right = insertIntoBST(root.right, val);
if (root.val > val)
root.left = insertIntoBST(root.left, val);
return root;
}
三、在 BST 中删除一个数
这个问题稍微复杂,不过你有框架指导,难不住你。跟插入操作类似,先“找”再“改”,先把框架写出来再说:
TreeNode deleteNode(TreeNode root, int key) {
if (root.val == key) {
// 找到啦,进行删除
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
找到目标节点了,比方说是节点 A,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况,用图片来说明。
情况 1:A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
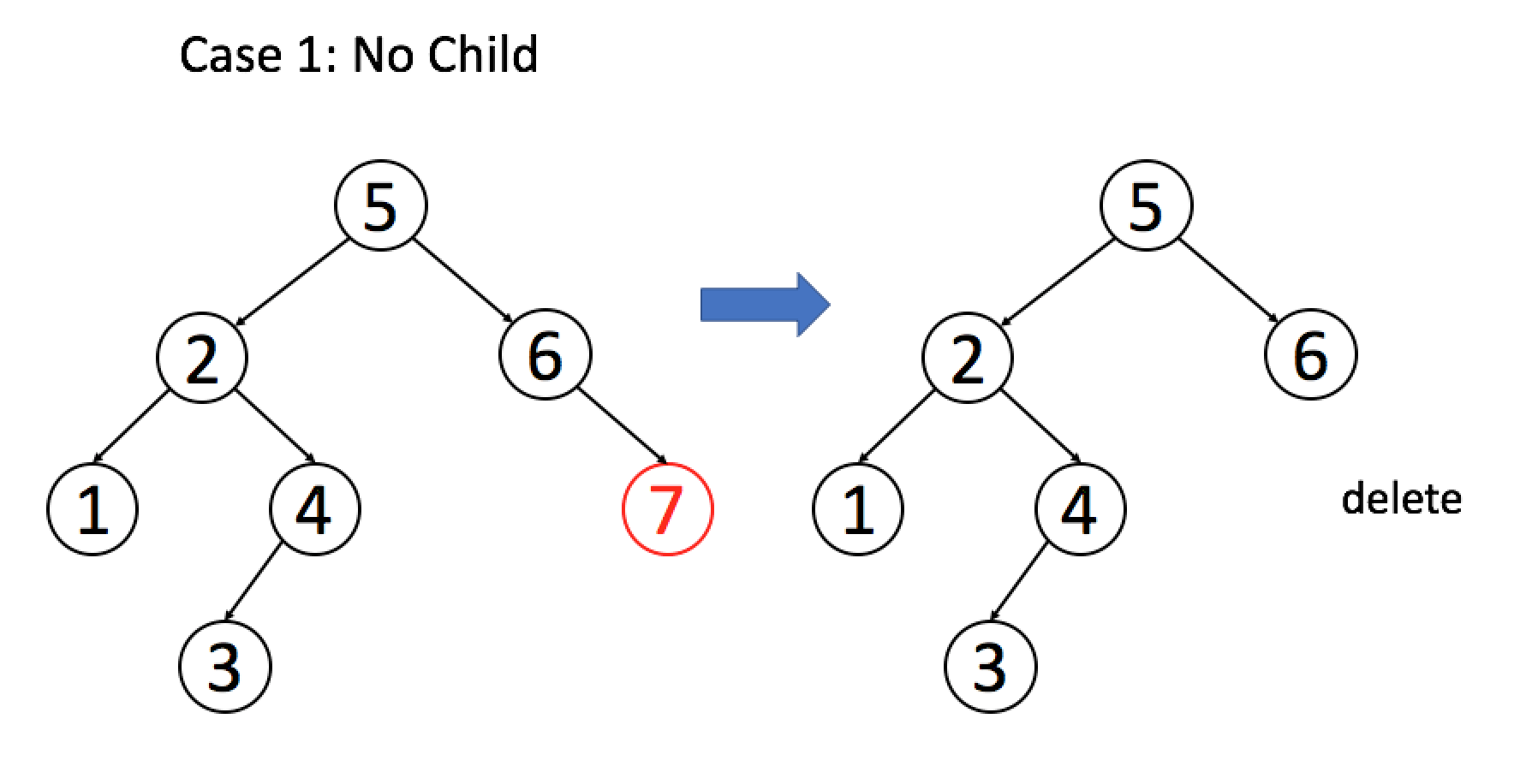
if (root.left == null && root.right == null)
return null;
情况 2:A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
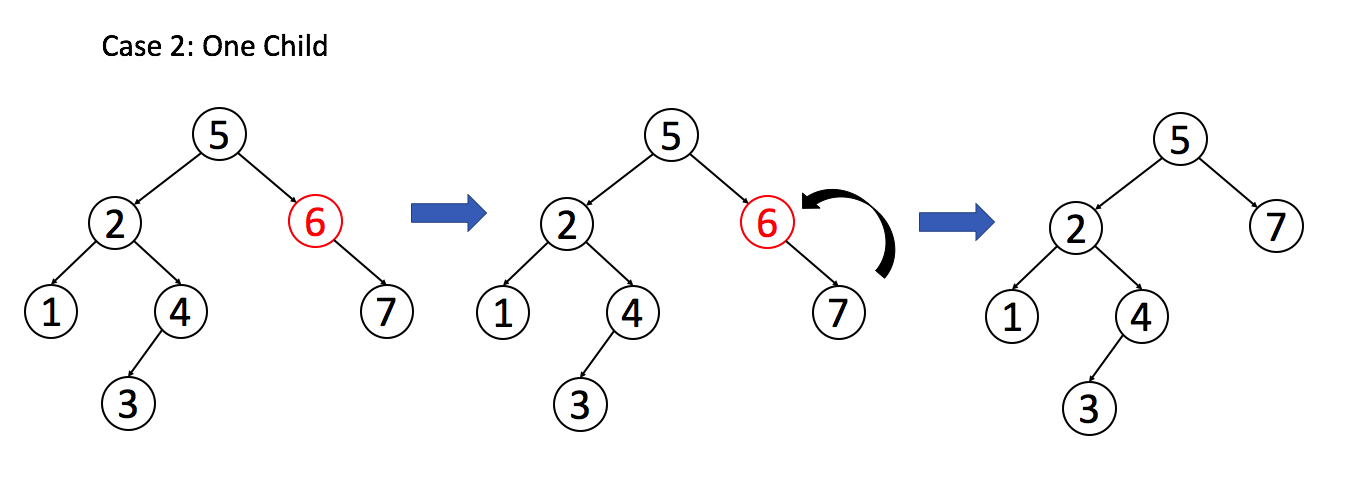
// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;
情况 3:A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。关注我的众公号 labuladong 看更多精彩算法文章~

if (root.left != null && root.right != null) {
// 找到右子树的最小节点
TreeNode minNode = getMin(root.right);
// 把 root 改成 minNode
root.val = minNode.val;
// 转而去删除 minNode
root.right = deleteNode(root.right, minNode.val);
}
三种情况分析完毕,填入框架,简化一下代码:
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 处理情况 3
TreeNode minNode = getMin(root.right);
root.val = minNode.val;
root.right = deleteNode(root.right, minNode.val);
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node) {
// BST 最左边的就是最小的
while (node.left != null) node = node.left;
return node;
}
删除操作就完成了。注意一下,这个删除操作并不完美,因为我们一般不会通过 root.val = minNode.val 修改节点内部的值来交换节点,而是通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应用中,val 域可能会很大,修改起来很耗时,而链表操作无非改一改指针,而不会去碰内部数据。
但这里忽略这个细节,旨在突出 BST 基本操作的共性,以及借助框架逐层细化问题的思维方式。
四、最后总结
通过这篇文章,你学会了如下几个技巧:
-
二叉树算法设计的总路线:把当前节点要做的事做好,其他的交给递归框架,不用当前节点操心。
-
如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
-
在二叉树框架之上,扩展出一套 BST 遍历框架:
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
206. 反转链表
- 难度:
简单 - 本题涉及算法:
迭代递归 - 思路:
迭代递归 - 类似题型:
题目 206. 反转链表
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
方法一 迭代
解题思路
通过迭代 将 1->2->3->4->5->∮ 转换成 ∮<-1<-2<-3<-4<-5
如图执行过程:
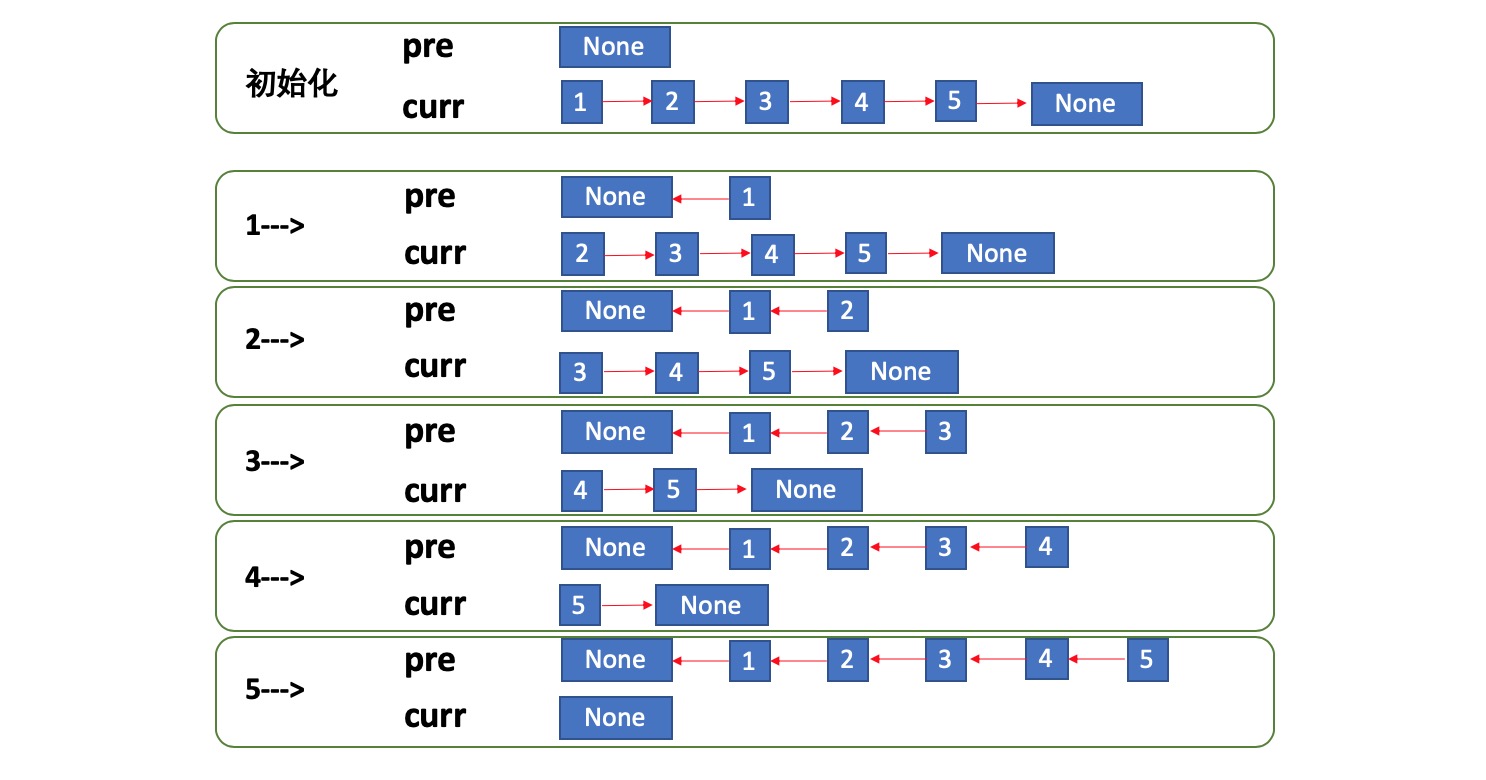
python
class Solution(object):
def reverseList(self, head):
# 申请两个链表 一个空链表,一个完整的链表
pre = None
curr = head
while curr:
temp = curr.next
curr.next = pre # 当前链表指向 新链表
pre = curr # 赋值给新链表
curr = temp
return pre
java
class Solution {
public ListNode reverseList(ListNode head) {
// 申请两个链表 一个空链表,一个完整的链表
ListNode pre = null;
ListNode curr = head;
while (curr!=null){
ListNode temp = curr.next;
curr.next = pre; // 当前链表指向 新链表
pre = curr; // 赋值给新链表
curr = temp;
}
return pre;
}
}
迭代升级版
python
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
cur , prev = head, None
while cur:
cur.next ,prev, cur = prev, cur , cur.next
return prev
递归
解题思路
- 终止条件是当前节点或者下一个节点==null
- 在函数内部,改变节点的指向,也就是 head 的下一个节点指向 head 递归函数那句
head.next.next = head
ListNode cur = reverseList(head.next); // 当head=4 head.next->5
if(head==null || head.next==null) { // head.next ->null 即 5.next = null
return head; // head = 5
}
- 所以 cul =5
- head.next.next = head; 中head = 4
- 即 4.next.next = 4
- 即 5.next = 4
java
class Solution {
public ListNode reverseList(ListNode head) {
//递归终止条件是当前为空,或者下一个节点为空
if(head==null || head.next==null) {
return head;
}
//这里的cur就是最后一个节点
ListNode cur = reverseList(head.next);
//如果链表是 1->2->3->4->5,那么此时的cur就是5
//而head是4,head的下一个是5,下下一个是空
//所以head.next.next 就是5->4
head.next.next = head;
//防止链表循环,需要将head.next设置为空
head.next = null;
//每层递归函数都返回cur,也就是最后一个节点
return cur;
}
}
python
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
# 递归终止条件是当前为空,或者下一个节点为空
if(head==None or head.next==None):
return head
# 这里的cur就是最后一个节点
cur = self.reverseList(head.next)
# 如果链表是 1->2->3->4->5,那么此时的cur就是5
# 而head是4,head的下一个是5,下下一个是空
# 所以head.next.next 就是5->4
head.next.next = head
# 防止链表循环,需要将head.next设置为空
head.next = None
# 每层递归函数都返回cur,也就是最后一个节点
return cur
方法三 栈
- 通过遍历把链表元素添加到栈内存
- 在把栈里面数据挨个添加到新的链表中
java
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null) {
return null;
}
// 遍历链表到栈内存
Stack<Integer> stack = new Stack<>();
ListNode ans = null;
while (head != null) {
stack.push(head.val);
head = head.next;
}
ListNode reverseListHead = new ListNode(stack.pop()); // 初始化链表首个元素
ListNode tempNode = reverseListHead;
while (!stack.isEmpty()) {
tempNode.next = new ListNode(stack.pop());
tempNode = tempNode.next;
}
return reverseListHead;
}
}
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
98. 验证二叉搜索树
- 难度:
中等 - 本题涉及算法:
中序遍历 - 思路:
中序遍历 - 类似题型:
题目 98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
方法一
解题思路
- 中序遍历时,判断当前节点是否大于中序遍历的前一个节点,如果大于,说明满足 BST,继续遍历;否则直接返回 false。
java
class Solution { long pre = Long.MIN_VALUE; public boolean isValidBST(TreeNode root) { if (root == null) { return true; } // 访问左子树 if (!isValidBST(root.left)) { return false; } // 访问当前节点:如果当前节点小于等于中序遍历的前一个节点,说明不满足BST,返回 false;否则继续遍历。 if (root.val <= pre) { return false; } pre = root.val; // 访问右子树 return isValidBST(root.right); } }
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 中序遍历 : 按照 左 中 右 的顺序 挨个遍历
class Solution:
cur = float("-inf")
def isValidBST(self, root: TreeNode) -> bool:
if root is None:
return True
# 访问左子树
if not self.isValidBST(root.left):
return False
# 访问当前节点:如果当前节点小于等于中序遍历的前一个节点,说明不满足BST,返回 false;否则继续遍历。
if (root.val <= self.cur):
return False
self.cur = root.val
# 访问右子树
return self.isValidBST(root.right)
1438. 绝对差不超过限制的最长连续子数组
- 难度:
中等 - 本题涉及算法:
滑动窗口 - 思路:
滑动窗口 - 类似题型:
题目 1438. 绝对差不超过限制的最长连续子数组
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
输入:nums = [8,2,4,7], limit = 4
输出:2
解释:所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。
示例 2:
输入:nums = [10,1,2,4,7,2], limit = 5
输出:4
解释:满足题意的最长子数组是 [2,4,7,2],其最大绝对差 |2-7| = 5 <= 5 。
示例 3:
输入:nums = [4,2,2,2,4,4,2,2], limit = 0
输出:3
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9
方法一 滑动窗口
解题思路
- 维护一直最大值和最小值
-
维护一个最长数组 \(sub\_nums增加的条件=\begin{cases} abs(num - curr\_max) <= limit & 判断当前元素是否复合条件,当前元素和数组中最大元素比较\\ abs(num - curr\_min) <= limit & 判断当前元素是否复合条件,当前元素和数组中最小元素比较 \\ abs(curr\_max - curr\_min) <= limit & 判断数组中元素是否符合条件,数组中最大元素和最小元素比较 \end{cases}\)
- 当不复合数组增加条件,则以当前长度向后移动
- 在向后移动的同时,数组中元素也在在发生变化,所以需要更新数组中的最大最小值
执行过程 举例 nums = [10,1,2,4,7,2] limit = 5
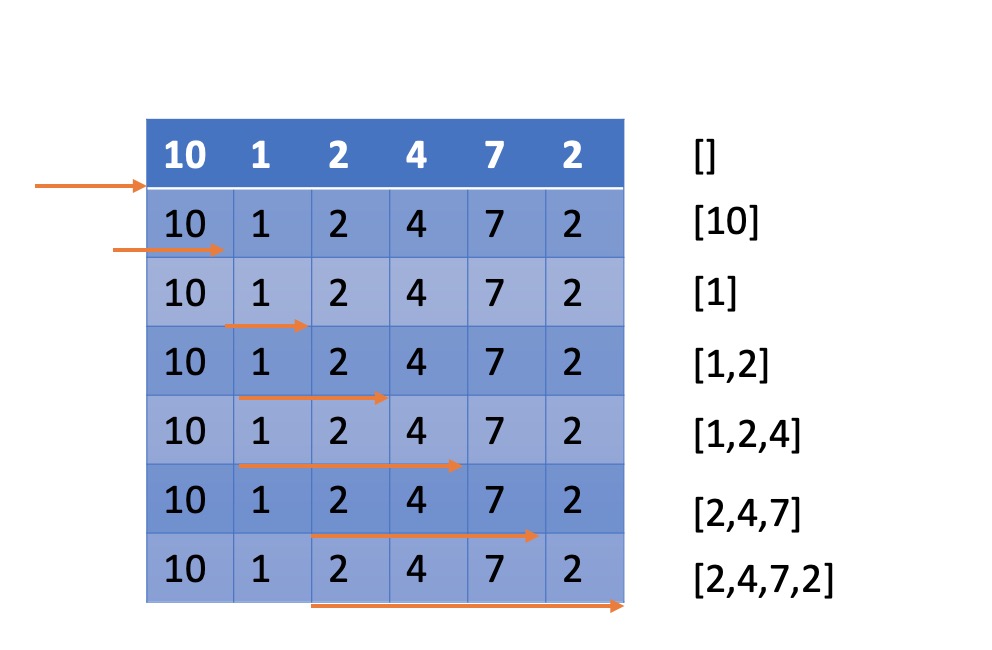
python
class Solution(object):
def longestSubarray(self, nums, limit):
if not nums:
return 0
curr_max = nums[0] # 当子数组下最大值 这里初始化为第一个数
curr_min = nums[0] # 当子数组下最大值 这里初始化为第一个数
sub_nums = [] # 以数组作为窗口滑动
for num in nums:
if abs(num - curr_max) <= limit and abs(num - curr_min) <= limit and abs(curr_max - curr_min) <= limit:
curr_max = max(num,curr_max)
curr_min = min(num,curr_min)
sub_nums.append(num)
else:
sub_nums.append(num)
sub_nums.pop(0)
curr_max = max(sub_nums) # 当子数组最大值
curr_min = min(sub_nums) # 当前子数组最小值
return len(sub_nums)
java
class Solution {
public int longestSubarray(int[] nums, int limit) {
if (nums ==null || nums.length==0)
return 0;
int curr_max = nums[0]; // 当子数组下最大值 这里初始化为第一个数
int curr_min = nums[0]; // 当子数组下最大值 这里初始化为第一个数
Queue<Integer> sub_nums = new LinkedList<>();
for(int num:nums){
if (Math.abs(num - curr_max) <= limit && Math.abs(num - curr_min) <= limit && Math.abs(curr_max - curr_min) <= limit) {
curr_max = Math.max(num,curr_max);
curr_min = Math.min(num,curr_min);
sub_nums.offer(num);
}else{
sub_nums.offer(num);
sub_nums.poll();
curr_max = Collections.max(sub_nums); // 当子数组最大值
curr_min = Collections.min(sub_nums); // 当前子数组最小值
}
}
return sub_nums.size();
}
}
错误代码
本想设计一个 时间复杂度为 n 的 结果错了 尴尬
- 错误答案 错在 [10,1,2,4,7,2] 5
class Solution(object): def longestSubarray(self, nums, limit): """ :type nums: List[int] :type limit: int :rtype: int """ if not nums: return 0 curr_max = nums[0] # 当子数组下最大值 这里初始化为第一个数 curr_min = nums[0] # 当子数组下最大值 这里初始化为第一个数 len_max = 0 # 最长子数组长度 len_curr = 0 # 当前子数组长度 for num in nums: if abs(num - curr_max) < limit and abs(num - curr_min) < limit: curr_max = max(num,curr_max) curr_min = min(num,curr_min) len_curr += 1 else: len_max = max(len_max,len_curr) curr_max = num # 下一个子数组当前最大值 curr_min = num # 下一个子数组当前最小值 len_curr = 1 # 因为该下标已经计算过一次 所以 设置当前子数组长度为 1 return max(len_max,len_curr) # 当数组中所有数都满足条件 则len_max,len_curr 进行比较
滑动窗口
文案
TODO
常用场景的一些总结
- 数组顺序不能改变
- 需要求的答案也通常是连续在一起
- 通常会给一个限定条件
类似题目
滑动窗口 通用代码
def move(self,nums,limit):
二叉树的先序、中序、后序遍历
大概的概念
二叉树的遍历分为两种:深度优先遍历和广度优先遍历;深度优先遍历又分为三种,先序、中序和后序
- 所有例子都是基于以下树进行遍历的
- 后面有类似题型

深度优先遍历(辅助结构:栈)
先序遍历
根节点,左子树,右子树
结果:124563
中序遍历
左子树,根节点,右子树
结果:425613
后序遍历
左子树,右子树,根节点
结果:465231
关于先序、中序、后序遍历,我只说一点:就是这里的先、中、后指的是根节点,根节点,根节点。。。。
广度优先遍历(辅助结构:队列)
很简单,结果为:123456
补充一下:广度优先遍历又叫层次遍历,感觉这个名字更加形象点,另外,每次遍历完一个节点会将它的子节点做入队操作。
类似题目
二叉树(前序,中序,后序,层序)遍历递归与循环的python实现
二叉树的遍历是在面试使比较常见的项目了。对于二叉树的前中后层序遍历,每种遍历都可以递归和循环两种实现方法,且每种遍历的递归实现都比循环实现要简洁。下面做一个小结。
一、中序遍历
前中后序三种遍历方法对于左右结点的遍历顺序都是一样的(先左后右),唯一不同的就是根节点的出现位置。对于中序遍历来说,根结点的遍历位置在中间。
所以中序遍历的顺序:左中右
1.1 递归实现
每次递归,只需要判断结点是不是None,否则按照左中右的顺序打印出结点value值。
class Solution:
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root:
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
1.2 循环实现
循环比递归要复杂得多,因为你得在一个函数中遍历到所有结点。但是有句话很重要:
对于树的遍历,循环操作基本上要用到栈(stack)这个结构
对于中序遍历的循环实现,每次将当前结点(curr)的左子结点push到栈中,直到当前结点(curr)为None。这时,pop出栈顶的第一个元素,设其为当前结点,并输出该结点的value值,且开始遍历该结点的右子树。
例如,对于上图的一个二叉树,其循环遍历过程如下表:

| No. | 输出列表sol | 栈stack | 当前结点curr |
|---|---|---|---|
| 1 | [] | [] | 1 |
| 2 | [] | [1] | 2 |
| 3 | [] | [1,2] | 4 |
| 4 | [] | [1,2,4] | None |
| 5 | [4] | [1,2] | 4 -> None(4的右结点) |
| 6 | [4,2] | [1] | 2 -> 5 |
| 7 | [4,2] | [1,5] | None(5的左结点) |
| 8 | [4,2,5] | [1] | 5 -> None(5的右结点) |
| 9 | [4,2,5,1] | [] | 3 |
| 10 | [4,2,5,1] | [3] | None |
| 11 | [4,2,5,1,3] | [] | None |
可见,规律为:当前结点curr不为None时,每一次循环将当前结点curr入栈;当前结点curr为None时,则出栈一个结点,且打印出栈结点的value值。整个循环在stack和curr皆为None的时候结束。
class Solution:
def inorderTraversal(self, root):
stack = []
sol = []
curr = root
while stack or curr:
if curr:
stack.append(curr)
curr = curr.left
else:
curr = stack.pop()
sol.append(curr.val)
curr = curr.right
return sol
二、前序遍历和后序遍历
按照上面的说法,前序遍历指根结点在最前面输出,所以前序遍历的顺序是:中左右
后序遍历指根结点在最后面输出,所以后序遍历的顺序是:左右中
2.1 递归实现
递归实现与中序遍历几乎完全一样,改变一下打印的顺序即可:
class Solution:
def preorderTraversal(self, root): ##前序遍历
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root:
return []
return [root.val] + self.inorderTraversal(root.left) + self.inorderTraversal(root.right)
def postorderTraversal(self, root): ##后序遍历
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root:
return []
return self.inorderTraversal(root.left) + self.inorderTraversal(root.right) + [root.val]
改动的地方只有return时函数的打印顺序。
2.2 循环实现
为什么把前序遍历和后序遍历放在一起呢?Leetcode上前序遍历是medium难度,后序遍历可是hard难度呢!
实际上,后序遍历不就是前序遍历的“反过程”嘛!
先看前序遍历。我们仍然使用栈stack,由于前序遍历的顺序是中左右,所以我们每次先打印当前结点curr,并将右子结点push到栈中,然后将左子结点设为当前结点。入栈和出栈条件(当前结点curr不为None时,每一次循环将当前结点curr入栈;当前结点curr为None时,则出栈一个结点)以及循环结束条件(整个循环在stack和curr皆为None的时候结束)与中序遍历一模一样。
再看后序遍历。由于后序遍历的顺序是左右中,我们把它反过来,则遍历顺序变成中左右,是不是跟前序遍历只有左右结点的差异了呢?然而左右的差异仅仅就是.left和.right的差异,在代码上只有机械的差别。
我们来看代码:
class Solution:
def preorderTraversal(self, root): ## 前序遍历
stack = []
sol = []
curr = root
while stack or curr:
if curr:
sol.append(curr.val)
stack.append(curr.right)
curr = curr.left
else:
curr = stack.pop()
return sol
def postorderTraversal(self, root): ## 后序遍历
stack = []
sol = []
curr = root
while stack or curr:
if curr:
sol.append(curr.val)
stack.append(curr.left)
curr = curr.right
else:
curr = stack.pop()
return sol[::-1]
代码的主体部分基本就是.right和.left交换了顺序,且后序遍历在最后输出的时候进行了反向(因为要从中右左变为左右中)
三、层序遍历
层序遍历也可以叫做宽度优先遍历:先访问树的第一层结点,再访问树的第二层结点…然后一直访问到最下面一层结点。在同一层结点中,以从左到右的顺序依次访问。
3.1 递归实现
递归函数需要有一个参数level,该参数表示当前结点的层数。遍历的结果返回到一个二维列表sol=[[]]中,sol中的每一个子列表保存了对应index层的从左到右的所有结点value值。
class Solution:
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
def helper(node, level):
if not node:
return
else:
sol[level-1].append(node.val)
if len(sol) == level: # 遍历到新层时,只有最左边的结点使得等式成立
sol.append([])
helper(node.left, level+1)
helper(node.right, level+1)
sol = [[]]
helper(root, 1)
return sol[:-1]
PS:
Q:如果仍然按层遍历,但是每层从右往左遍历怎么办呢?
A:将上面的代码left和right互换即可
Q:如果仍然按层遍历,但是我要第一层从左往右,第二层从右往左,第三从左往右…这种zigzag遍历方式如何实现?
A:将 sol[level-1].append(node.val) 进行一个层数奇偶的判断,一个用 append(),一个用 insert(0,)
if level%2==1:
sol[level-1].append(node.val)
else:
sol[level-1].insert(0, node.val)
3.2 循环实现
这里的循环实现不能用栈了,得用队列queue。因为每一层都需要从左往右打印,而每打印一个结点都会在队列中依次添加其左右两个子结点,每一层的顺序都是一样的,故必须采用先进先出的数据结构。
以下代码的打印结果为一个一维列表,没有采用二维列表的形式。
class Solution:
def levelOrder(self, root):
if not root:
return []
sol = []
curr = root
queue = [curr]
while queue:
curr = queue.pop(0)
sol.append(curr.val)
if curr.left:
queue.append(curr.left)
if curr.right:
queue.append(curr.right)
return sol
其实,如果需要打印成zigzag形式(相邻层打印顺序相反),则可以采用栈stack数据结构,正好符合先进后出的形式。不过在代码上还要进行其他改动。
339 post articles, 43 pages.