199. 二叉树的右视图
- 难度:
中等 - 本题涉及算法:
DFSBFS - 思路:
DFSBFS - 类似题型:
题目 199. 二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
方法一 DFS
解题思路
- 我们按照 「根结点 -> 右子树 -> 左子树」 的顺序访问,就可以保证每层都是最先访问最右边的节点的
代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
// 考察的是对二叉数执行顺序
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
// 从根节点开始访问,根节点深度是0
dfs(root,0);
return res;
}
private void dfs(TreeNode root,int deepth){
if (root ==null) return;
// 先访问 当前节点,再递归地访问 右子树 和 左子树
if(deepth==res.size()) res.add(root.val);// 如果当前节点所在深度还没有出现在res里,说明在该深度下当前节点是第一个被访问的节点,因此将当前节点加入res中。
deepth++;
dfs(root.right,deepth);
dfs(root.left,deepth);
}
}
方法二 BFS
-
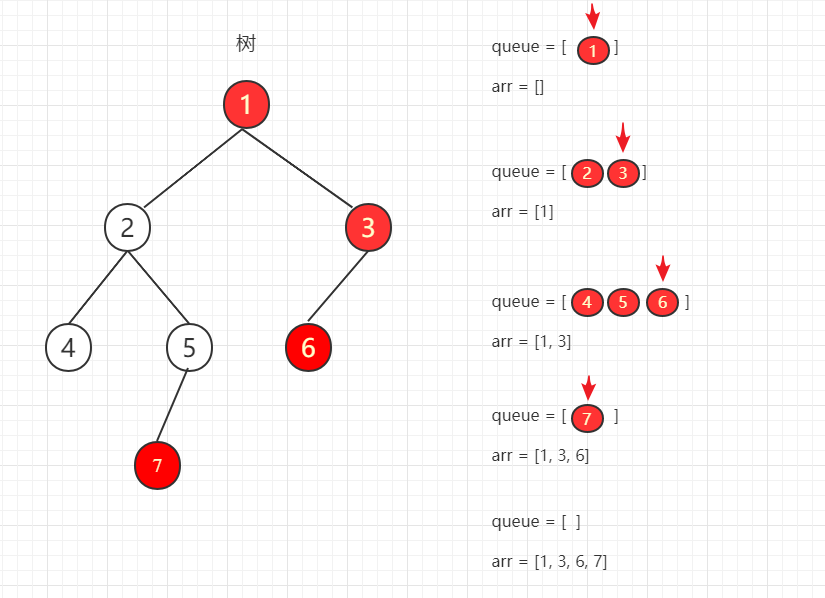
利用 BFS 进行层次遍历,记录下每层的最后一个元素。
-
二叉树插入队列的如图
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
// 考察的是对二叉数执行顺序
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size = queue.size();
for(int i = 0;i<size;i++){
TreeNode node = queue.poll();
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null) {
queue.offer(node.right);
}
if (i==size-1) {
res.add(node.val); //将当前层的最后一个节点放入结果列表
}
}
}
return res;
}
}
23. 合并K个排序链表
- 难度:
困难 - 本题涉及算法:
优先队列 - 思路:
优先队列 - 类似题型:
23. 合并K个排序链表
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
方法一 优先队列
解题思路
- 通过题目和示例,可清楚的了解到,其实就是 合并元素,并 排序
- 第一步通队列保存链表元素
- 对队列排序
- 通过优先队列,可完成上述两个步骤
Queue<Integer> queue = new PriorityQueue<>((i1, i2) -> Integer.compare(i2, i1));时间复杂度:$O(n*log(k))$,n 是所有链表中元素的总和,k 是链表个数
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
Queue<Integer> queue = new PriorityQueue<>((i1, i2) -> Integer.compare(i2, i1));
// 合并链表元素到队列
for(ListNode node:lists){
while (node != null){
queue.offer(node.val);
node = node.next;
}
}
// 把队列中元素添加到了新的链表
ListNode ans = null;
while (!queue.isEmpty()){
ListNode curr = new ListNode(queue.poll()); // 每次拿出最大元素,并删除
curr.next = ans;
ans = curr;
}
return ans;
}
}
213. 打家劫舍 II
- 难度:
中等 - 本题涉及算法:
动态规划 - 思路:
动态规划 - 类似题型:
题目 213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
方法一
解题思路
- 这次审题终于正确,🙆♂️
- 我们可以把题目分成两个部分
- 在 [0:n-1] 中找到最大值
- 在 [1:n] 中找到最大值
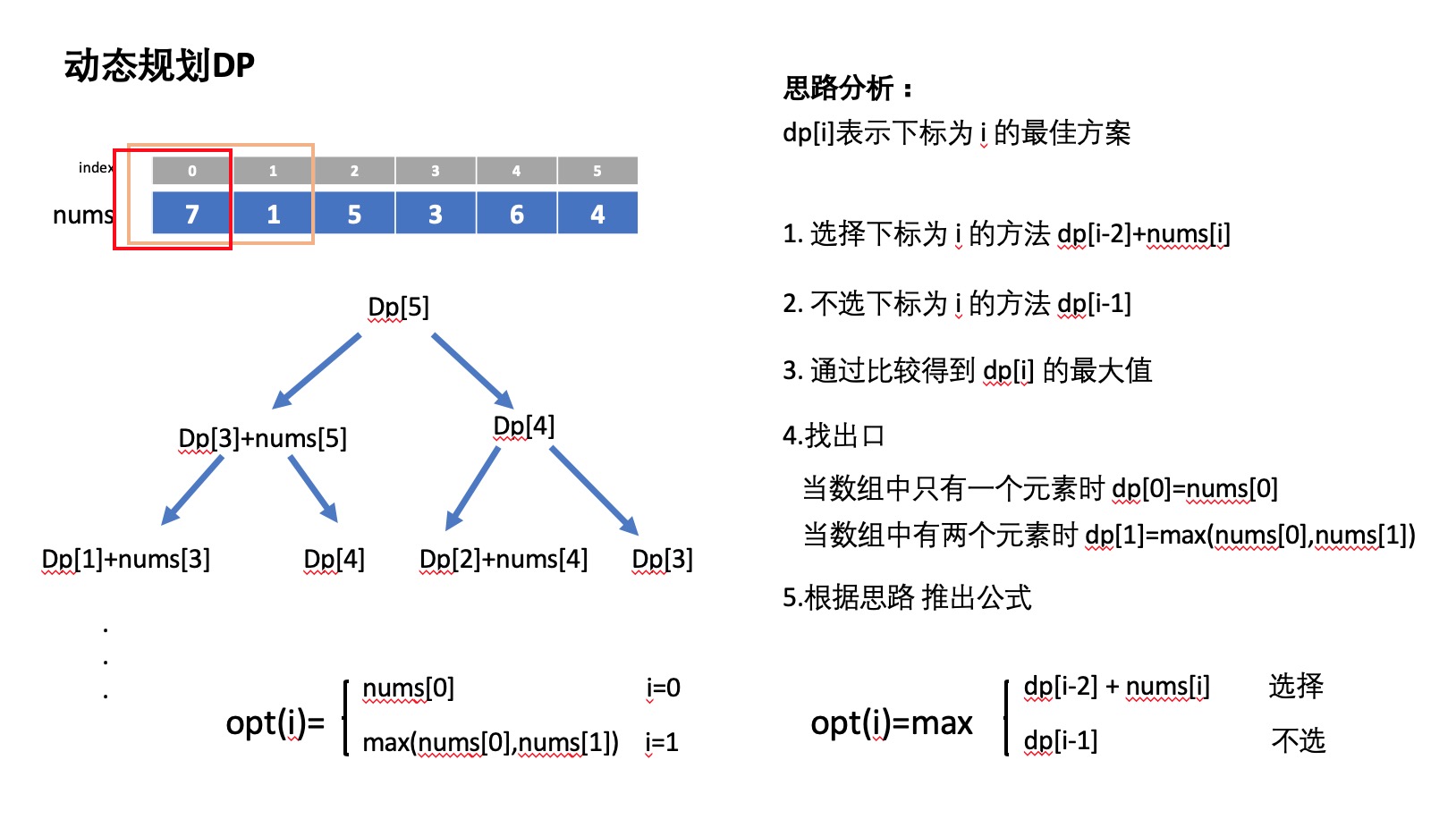
动态规划基本思路
- 如图
代码
class Solution:
def rob(self, nums: List[int]) -> int:
def robmax(nums):
nums_len = len(nums)
if not nums: return 0
if nums_len == 1: return nums[0]
opt = [0] * nums_len
opt[0] = nums[0]
opt[1] = max(nums[0],nums[1])
for i in range(2,nums_len):
opt[i] = max(opt[i-1],opt[i-2]+nums[i])
return opt[nums_len-1]
if not nums: return 0
if len(nums) == 1: return nums[0]
nums1 = nums[1:] #[1,n] 找到到最大值
nums2 = nums[0:len(nums)-1] # [0,n-1] 找到到最大值
return max(robmax(nums1),robmax(nums2))
class Solution {
public int rob(int[] nums) {
if(nums.length == 0) return 0;
if(nums.length == 1) return nums[0];
int[] nums1 = Arrays.copyOfRange(nums, 1, nums.length);
int[] nums2 = Arrays.copyOfRange(nums, 0, nums.length - 1);
return Math.max(subrob(nums1), subrob(nums2));
}
private int subrob(int[] nums){
int len = nums.length;
if (len == 0) return 0;
if (len == 1) return nums[0];
int[] dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < len; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[len - 1];
}
}
- 如果你觉得本文对你有帮助,请点赞👍支持
- 如果有疑惑或者表达不到位的额地方 ,请在下面👇评论区指出
图解动态规划的解题四步骤
- 类似题目:
图解动态规划的解题四步骤
如果你对于动态规划还不是很了解,或者没怎么做过动态规划的题目的话,那么 House Robber (小偷问题)这道题是一个非常好的入门题目。本文会以 House Robber 题目为例子,讲解动态规划题目的四个基本步骤。
动态规划的的四个解题步骤是:
- 定义子问题
- 写出子问题的递推关系
- 确定 DP 数组的计算顺序
- 空间优化(可选)
下面我们一步一步地进行讲解。
步骤一:定义子问题
稍微接触过一点动态规划的朋友都知道动态规划有一个“子问题”的定义。什么是子问题?子问题是和原问题相似,但规模较小的问题。例如这道小偷问题,原问题是“从全部房子中能偷到的最大金额”,将问题的规模缩小,子问题就是“从 k 个房子中能偷到的最大金额”,用 f(k) 表示。

可以看到,子问题是参数化的,我们定义的子问题中有参数 kk。假设一共有 nn 个房子的话,就一共有 nn 个子问题。动态规划实际上就是通过求这一堆子问题的解,来求出原问题的解。这要求子问题需要具备两个性质:
- 原问题要能由子问题表示。例如这道小偷问题中,k=nk=n 时实际上就是原问题。否则,解了半天子问题还是解不出原问题,那子问题岂不是白解了。
- 一个子问题的解要能通过其他子问题的解求出。例如这道小偷问题中,f(k)f(k) 可以由 f(k-1)f(k−1) 和 f(k-2)f(k−2) 求出,具体原理后面会解释。这个性质就是教科书中所说的“最优子结构”。如果定义不出这样的子问题,那么这道题实际上没法用动态规划解。
小偷问题由于比较简单,定义子问题实际上是很直观的。一些比较难的动态规划题目可能需要一些定义子问题的技巧。
步骤二:写出子问题的递推关系
这一步是求解动态规划问题最关键的一步。然而,这一步也是最无法在代码中体现出来的一步。在做题的时候,最好把这一步的思路用注释的形式写下来。做动态规划题目不要求快,而要确保无误。否则,写代码五分钟,找 bug 半小时,岂不美哉?
我们来分析一下这道小偷问题的递推关系:
假设一共有 nn 个房子,每个房子的金额分别是 H0, H1, …,Hn-1,子问题 f(k)f(k) 表示从前 k 个房子(即 H0, H1,…Hk-1,中能偷到的最大金额。那么,偷 k 个房子有两种偷法:
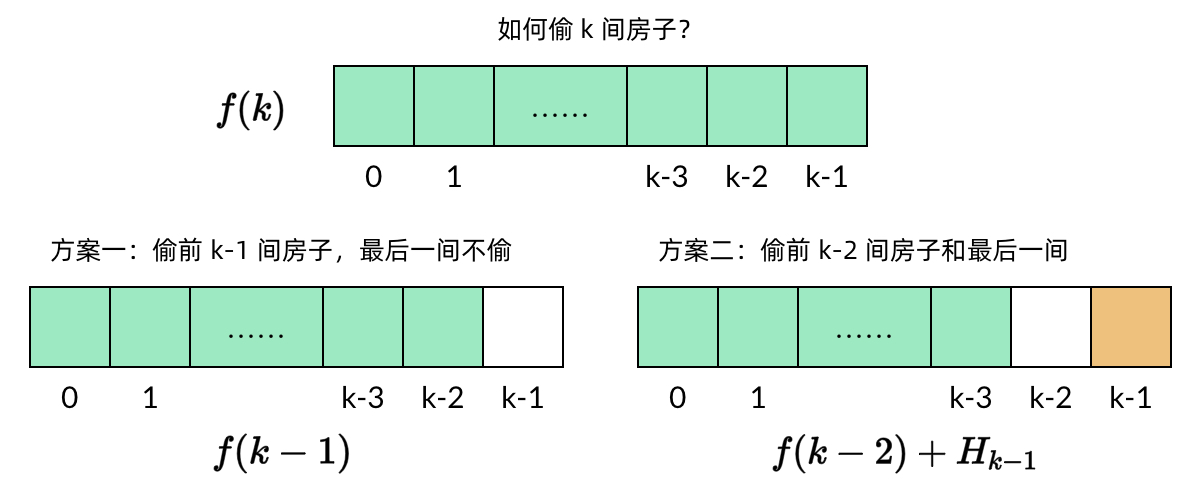
k 个房子中最后一个房子是 Hk-1。如果不偷这个房子,那么问题就变成在前 k-1个房子中偷到最大的金额,也就是子问题 f(k-1)。如果偷这个房子,那么前一个房子 Hk-2显然不能偷,其他房子不受影响。那么问题就变成在前 k-2 个房子中偷到的最大的金额。两种情况中,选择金额较大的一种结果。
f(k) = max{f(k-1), Hk-1 + f(k-2)}
在写递推关系的时候,要注意写上 k=0k=0 和 k=1k=1 的基本情况:
- 当 k=0 时,没有房子,所以 f(0) =0。
- 当 k=1 时,只有一个房子,偷这个房子即可,所以 f(1) = H0
这样才能构成完整的递推关系,后面写代码也不容易在边界条件上出错。
步骤三:确定 DP 数组的计算顺序
在确定了子问题的递推关系之后,下一步就是依次计算出这些子问题了。在很多教程中都会写,动态规划有两种计算顺序,一种是自顶向下的、使用备忘录的递归方法,一种是自底向上的、使用 dp 数组的循环方法。不过在 普通的动态规划题目中,99% 的情况我们都不需要用到备忘录方法,所以我们最好坚持用自底向上的 dp 数组。
DP 数组也可以叫”子问题数组”,因为 DP 数组中的每一个元素都对应一个子问题。如下图所示,dp[k] 对应子问题 f(k),即偷前 kk 间房子的最大金额。
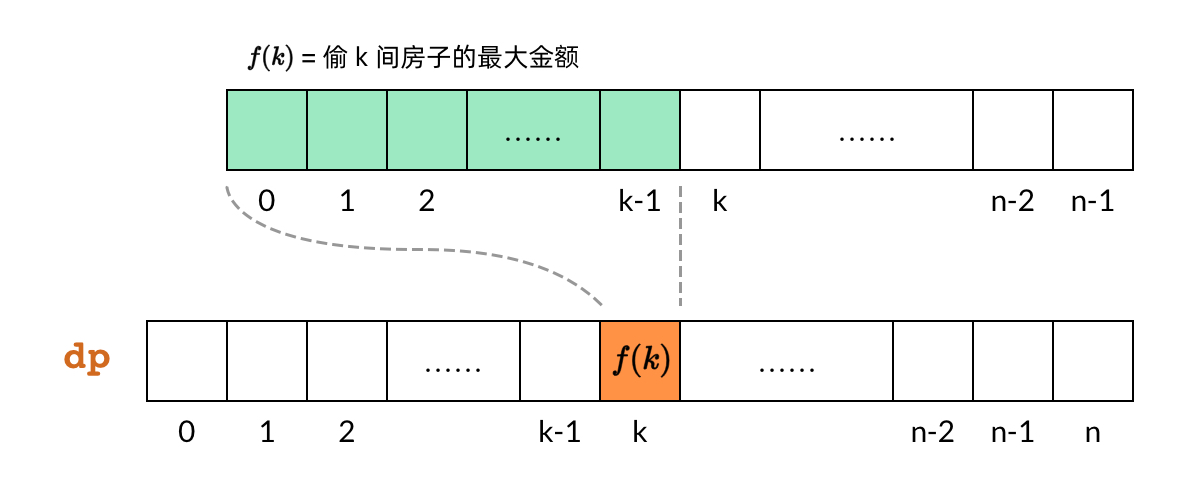
那么,只要搞清楚了子问题的计算顺序,就可以确定 DP 数组的计算顺序。对于小偷问题,我们分析子问题的依赖关系,发现每个 f(k) 依赖 f(k-1) 和 f(k−2)。也就是说,dp[k] 依赖 dp[k-1] 和 dp[k-2],如下图所示。
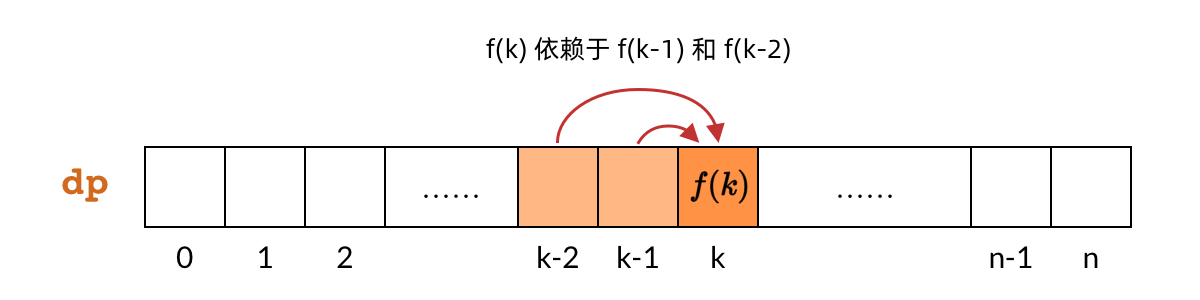
那么,既然 DP 数组中的依赖关系都是向右指的,DP 数组的计算顺序就是从左向右。这样我们可以保证,计算一个子问题的时候,它所依赖的那些子问题已经计算出来了。
确定了 DP 数组的计算顺序之后,我们就可以写出题解代码了:
Java:
public int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
// 子问题:
// f(k) = 偷 [0..k) 房间中的最大金额
// f(0) = 0
// f(1) = nums[0]
// f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }
int N = nums.length;
int[] dp = new int[N+1];
dp[0] = 0;
dp[1] = nums[0];
for (int k = 2; k <= N; k++) {
dp[k] = Math.max(dp[k-1], nums[k-1] + dp[k-2]);
}
return dp[N];
}
步骤四:空间优化
空间优化是动态规划问题的进阶内容了。对于初学者来说,可以不掌握这部分内容。
空间优化的基本原理是,很多时候我们并不需要始终持有全部的 DP 数组。对于小偷问题,我们发现,最后一步计算 f(n) 的时候,实际上只用到了 f(n-1) 和 f(n-2) 的结果。n-3 之前的子问题,实际上早就已经用不到了。那么,我们可以只用两个变量保存两个子问题的结果,就可以依次计算出所有的子问题。下面的动图比较了空间优化前和优化后的对比关系:
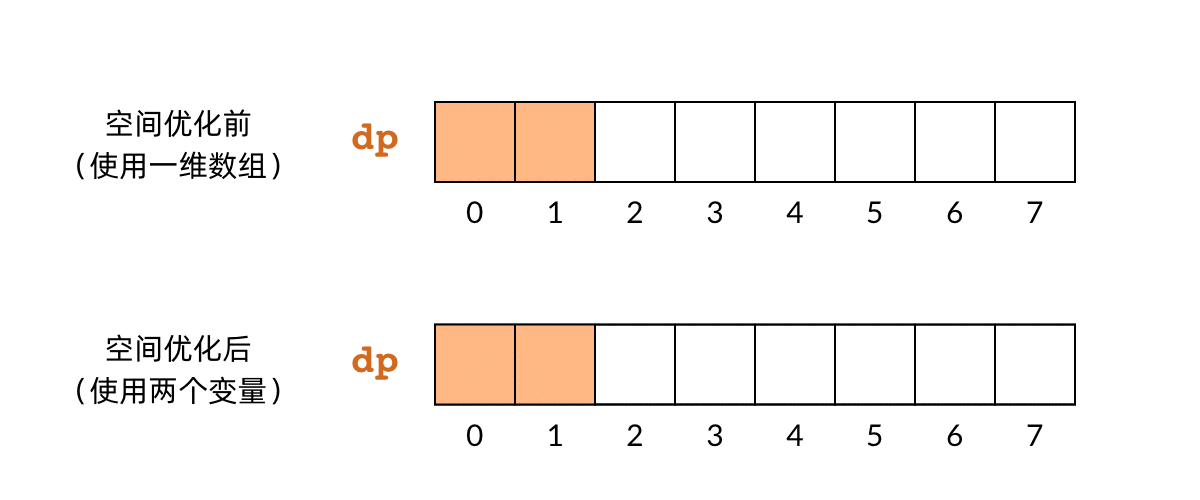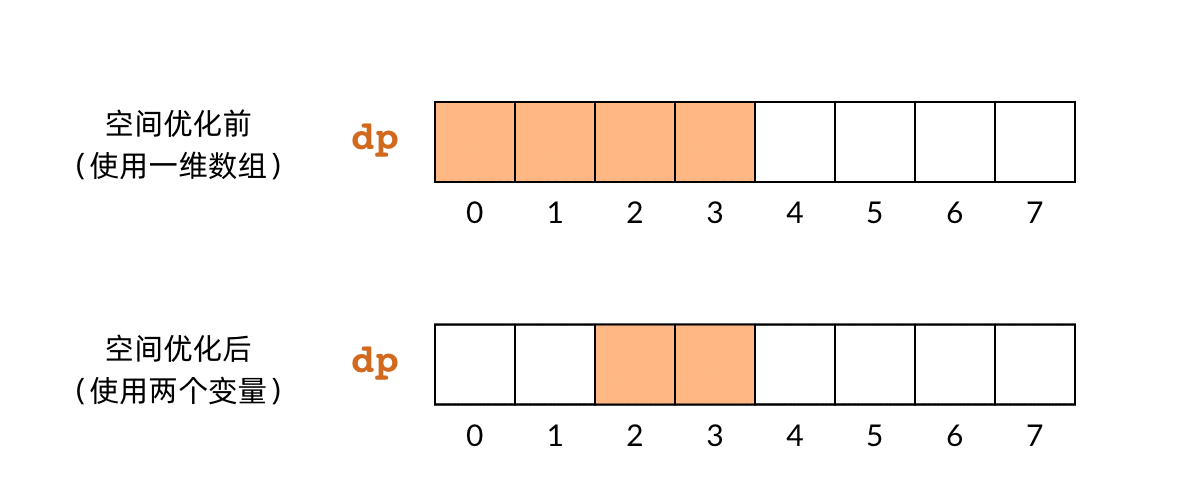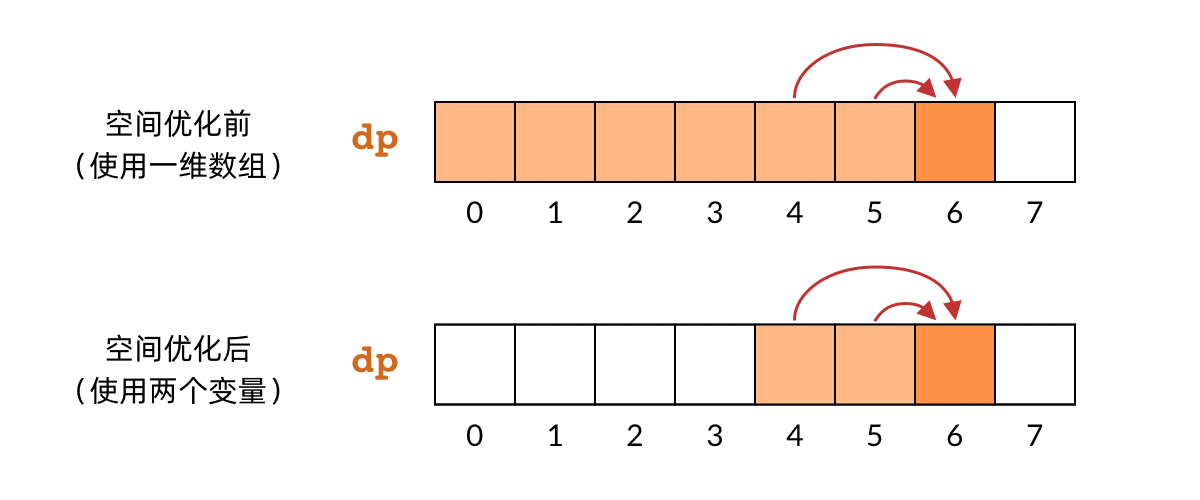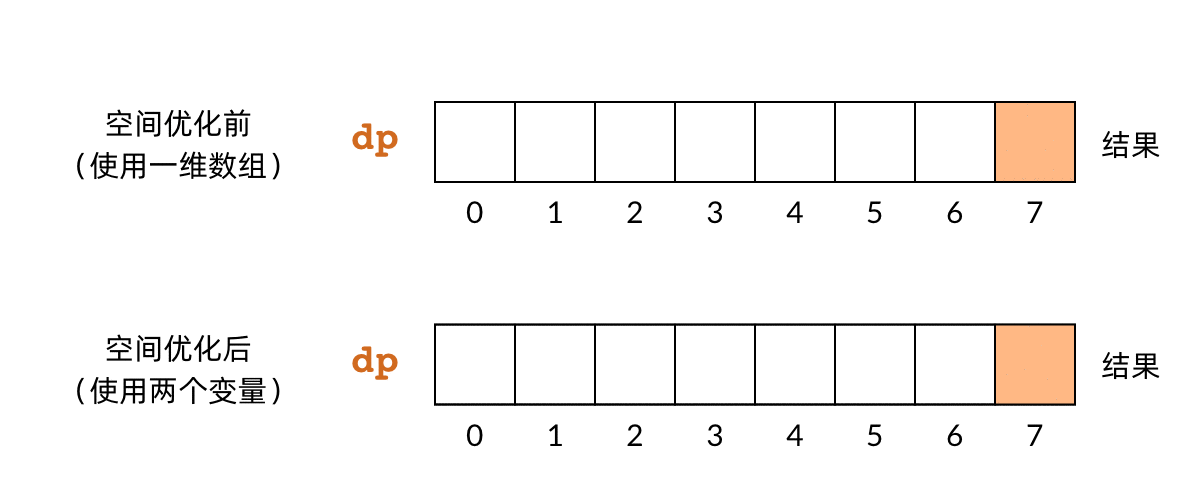
这样一来,空间复杂度也从 O(n)O(n) 降到了 O(1)O(1)。优化后的代码如下所示:
Java:
public int rob(int[] nums) {
int prev = 0;
int curr = 0;
// 每次循环,计算“偷到当前房子为止的最大金额”
for (int i : nums) {
// 循环开始时,curr 表示 dp[k-1],prev 表示 dp[k-2]
// dp[k] = max{ dp[k-1], dp[k-2] + i }
int temp = Math.max(curr, prev + i);
prev = curr;
curr = temp;
// 循环结束时,curr 表示 dp[k],prev 表示 dp[k-1]
}
return curr;
}
面试题68 - I. 二叉搜索树的最近公共祖先
- 难度:
简单 - 本题涉及算法:
迭代二叉树 - 思路:
迭代二叉树 - 类似题型:
题目 面试题68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大( 一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
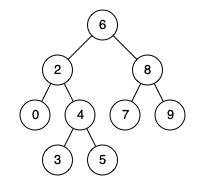
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
方法一 迭代
解题思路
- 祖先的定义: 若节点
p在节点root的左(右)子树中,或p = root,则称root是p的祖先。

最近公共祖先的定义: 设节点 root 为节点 p, q 的某公共祖先,若其左子节点 root.left 和右子节点 root.right 都不是 p,q 的公共祖先,则称 root 是 “最近的公共祖先” 。
根据以上定义,若 root 是 p, q 的 最近公共祖先 ,则只可能为以下情况之一:
p和q在 root 的子树中,且分列root的 异侧(即分别在左、右子树中);p = root,且q在root的左或右子树中;q = root,且p在root的左或右子树中;

本题给定了两个重要条件:① 树为 二叉搜索树 ,② 树的所有节点的值都是 唯一 的。根据以上条件,可方便地判断 p,q 与 root 的子树关系,即:
- 若
root.val < p.val,则p在root右子树 中; - 若
root.val > p.val,则p在root左子树 中; - 若
root.val = p.val,则p和root指向 同一节点 。
方法一:迭代
- 循环搜索: 当节点
root为空时跳出;- 当
p, q都在root的 右子树 中,则遍历至root.right; - 否则,当
p, q都在root的 左子树 中,则遍历至root.left; - 否则,说明找到了 最近公共祖先 ,跳出。
- 当
- 返回值: 最近公共祖先
root。
代码
java
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root != null) {
if(root.val < p.val && root.val < q.val) // p,q 都在 root 的右子树中
root = root.right; // 遍历至右子节点
else if(root.val > p.val && root.val > q.val) // p,q 都在 root 的左子树中
root = root.left; // 遍历至左子节点
else break;
}
return root;
}
}
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if p.val > q.val: p,q = q,p # 保证 p.val < q.val
while root:
if root.val < p.val:
root = root.right # 右子数
elif root.val > q.val:
root = root.left # 左子数
else:
break
return root
方法二 递归
# 递归
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if not root: return
if root.val < p.val and root.val < q.val:
root = self.lowestCommonAncestor(root.right,p,q)
if root.val > q.val and root.val > p.val:
root = self.lowestCommonAncestor(root.left,p,q)
return root
9. 回文数
- 难度:
简单 - 本题涉及算法:
算数双向指针 - 思路:
算数双向指针 - 类似题型:
题目 9. 回文数
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
示例 1:
输入: 121
输出: true
示例 2:
输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。
进阶:
你能不将整数转为字符串来解决这个问题吗?
方法一 算数
- 解题思路:
- 数值反转
- 复杂度分析:
- 时间复杂度 $O(n)$ ,$N$ 表示数值包含元素长度
- 空间复杂度 $O(1)$
java
class Solution {
public boolean isPalindrome(int x) {
if(x < 0) // 如果为负数,直接返回 false
return false;
int cur = 0;
int num = x;
while(num != 0) {
cur = cur * 10 + num % 10;
num /= 10;
}
return cur == x; // 最后比较 数值反转前后是否相等
}
}
python
class Solution:
def isPalindrome(self, x: int) -> bool:
if x < 0: # 如果为负数,直接返回 false
return False
num = x
cur = 0
while num !=0:
cur = cur*10 + num%10
num //=10
return cur == x # 最后比较 数值反转前后是否相等
方法二 双向指针
- 解题思路:
- 数值转成字符串,遍历元素
- 首尾各一个指针,向中间靠拢,每次元素是否相等
- 复杂度分析:
- 时间复杂度 $O(n/2)$ ,$N$ 表示数值包含元素长度 ,如果数值是回文数 最多需要遍历 $O(n/2)$ 次
- 时间复杂度 $O(1)$
java
class Solution {
public boolean isPalindrome(int x) {
if(x<0){ // 如果为负数,直接返回 false
return false;
}
String strNum = String.valueOf(x);
for(int i = 0;i<=strNum.length()/2;i++) {
int a = strNum.charAt(i);
int b = strNum.charAt(strNum.length()-1-i);
if(a != b) {
return false;
}
}
return true;
}
}
python
class Solution(object):
def isPalindrome(self, x):
nums = str(x)
for i in range(len(nums)):
if nums[i] != nums[len(nums)-1-i]:
return False
return True
方法三 取出后半段数字进行翻转
- 解题思路具体步骤
- 每次进行取余操作 ( %10),取出最低的数字:
y = x % 10 - 将最低的数字加到取出数的末尾:
revertNum = revertNum * 10 + y - 每取一个最低位数字,x 都要自除以 10
- 判断 x 是不是小于
revertNum,当它小于的时候,说明数字已经对半或者过半了 - 最后,判断奇偶数情况:如果是偶数的话,revertNum 和 x 相等;如果是奇数的话,最中间的数字就在revertNum 的最低位上,将它除以 10 以后应该和 x 相等。
- 每次进行取余操作 ( %10),取出最低的数字:
- 主要事项
- 这里需要注意的一个点就是由于回文数的位数可奇可偶,所以当它的长度是偶数时,它对折过来应该是相等的;当它的长度是奇数时,那么它对折过来后,有一个的长度需要去掉一位数(除以 10 并取整)。
- 复杂度分析:
- 时间复杂度 $O(n/2)$ ,$N$ 表示数值包含元素长度 ,如果数值是回文数 最多需要遍历 $O(n/2)$ 次
- 时间复杂度 $O(1)$
class Solution {
public boolean isPalindrome(int x) {
//思考:这里大家可以思考一下,为什么末尾为 0 就可以直接返回 false
if (x < 0 || (x % 10 == 0 && x != 0)) return false;
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
return x == revertedNumber || x == revertedNumber / 10;
}
}
572. 另一个树的子树
- 难度:
简单 - 本题涉及算法:
递归 - 思路:
递归 - 类似题型:
题目 572. 另一个树的子树
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1:
给定的树 s:
3
/ \
4 5
/ \
1 2
给定的树 t:
4
/ \
1 2
返回 true,因为 t 与 s 的一个子树拥有相同的结构和节点值。
示例 2:
给定的树 s:
3
/ \
4 5
/ \
1 2
/
0
给定的树 t:
4
/ \
1 2
返回 false。
解题思路
要判断一个树 t 是不是树 s 的子树,那么可以判断 t 是否和树 s 的任意子树相等。那么就转化成 100. 相同的树。 即,这个题的做法就是在 s 的每个子节点上,判断该子节点是否和 t 相等。
判断两个树是否相等的三个条件是与的关系,即:
- 当前两个树的根节点值相等;
- 并且,s 的左子树和 t 的左子树相等;
- 并且,s 的右子树和 t 的右子树相等。
而判断 t 是否为 s 的子树的三个条件是或的关系,即:
- 当前两棵树相等;
- 或者,t 是 s 的左子树;
- 或者,t 是 s 的右子树。
代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
// 递归的结束条件
if(s == null && t == null)
return true;
if (s == null || t == null)
return false;
return subTree(s,t) || isSubtree(s.left,t) || isSubtree(s.right,t);
}
public boolean subTree(TreeNode s,TreeNode t) {
// 递归的结束条件
if(s == null && t == null)
return true;
if (s == null || t == null)
return false;
return s.val==t.val && subTree(s.left, t.left) && subTree(s.right,t.right);
}
}
python
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def isSubtree(self, s, t):
"""
:type s: TreeNode
:type t: TreeNode
:rtype: bool
"""
if not s and not t:
return True
if not s or not t:
return False
return self.isSameTree(s, t) or self.isSubtree(s.left, t) or self.isSubtree(s.right, t)
def isSameTree(self, s, t):
if not s and not t:
return True
if not s or not t:
return False
return s.val == t.val and self.isSameTree(s.left, t.left) and self.isSameTree(s.right, t.right)
508. 出现次数最多的子树元素和
- 难度:
中等 - 本题涉及算法:
递归哈希表 - 思路:
递归哈希表 - 类似题型:
题目 508. 出现次数最多的子树元素和
给你一个二叉树的根结点,请你找出出现次数最多的子树元素和。一个结点的「子树元素和」定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。
你需要返回出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的子树元素和(不限顺序)。
示例 1:
输入:
5
/ \
2 -3
返回 [2, -3, 4],所有的值均只出现一次,以任意顺序返回所有值。
示例 2:
输入:
5
/ \
2 -5
返回 [2],只有 2 出现两次,-5 只出现 1 次。
提示: 假设任意子树元素和均可以用 32 位有符号整数表示。
方法一 递归+哈希表
解题思路
- 考察的其实还是对二叉树的理解 可参考 写树算法的套路框架
代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
// 配合map 记录最多出现次数的子树
private int max = 0;
public int[] findFrequentTreeSum(TreeNode root) {
if (root == null)
return new int[0];
Map<Integer, Integer> map = new HashMap<>();
helper(root, map);
// 然后求出map中value最大值对应的Key
List<Integer> res = new LinkedList<>();
for (Integer i : map.keySet()) {
if (map.get(i) == max)
res.add(i);
}
// 转数组
int[] resArr = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
resArr[i] = res.get(i);
}
return resArr;
}
public int helper(TreeNode root, Map<Integer, Integer> map) {
if (root == null)
return 0;
int left = helper(root.left, map);
int right = helper(root.right, map);
// 当前节点为根的元素和
int val = left + right + root.val;
map.put(val, map.getOrDefault(val, 0) + 1);
max = Math.max(max, map.get(val));
return val;
}
}
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
# 生成默认的字典 相当于 java中的 Map.getOrDefault(key,0)
tree_dict = collections.defaultdict(int)
# 递归 遍历出所有 子的元素和 并用 字典记录
def helper(root):
if not root:return 0
left = helper(root.left)
right = helper(root.right)
temp = left + right + root.val
tree_dict[temp] += 1
return temp
if not root:return []
helper(root)
# 记录出现最多次的 子树的元素和
tree_max = 0
# python 通过 dict.values() 遍历出字典中的 value
# 类似于 java中的 for(Map.Entry<String, String> entry : map.entrySet())
for cnt in tree_dict.values():
tree_max = max(cnt,tree_max)
res_list = []
# python 通过 dict.items() 遍历出字典中的key 和 value
for key, val in tree_dict.items():
if val == tree_max:
res_list.append(key)
return res_list
339 post articles, 43 pages.