JAVA 牛牛

Home

有nativeQuery = true和没有的区别

有 nativeQuery = true 时，是可以执行原生sql语句，所谓原生sql，也就是说这段sql拷贝到数据库中，然后把参数值给一下就能运行了，比如：

@Query(value = "select * from product_rel where audit_id=?1 and process_object=0 ",nativeQuery = true)
List<ProductRel> findAllByProductAuditId(Integer id);

这个时候，把 select * from product_rel where audit_id=?1 and process_object=0 拷贝到数据库中，并给audit_id赋一个值，那么这段sql就可以运行。其中数据库表在数据库中的表名就是product_rel，字段audit_id在数据库中也是真实存在的字段名。

 

没有 nativeQuery = true 时，就不是原生sql，而其中的 select * from xxx中xxx 也不是数据库对应的真正的表名，而是对应的实体名，并且sql中的字段名也不是数据库中真正的字段名，而是 实体的字段名。例如：

@Query("select ratio from MdmRatio ratio  where enabledNum=1 ")
List<MdmUtilThreeProjection> findByMdmUtilThreeProjection();

@Entity
@Table(name="mdm_ratio")
public class MdmRatio implements Serializale{...}

此中， select ratio from MdmRatio ratio 中的MdmRatio为实体名，不是真正的数据库表名，真正的数据库表名是mdm_ratio(如上图@Table里面写的那样，MdmRatio实体对应的数据库表名是mdm_ratio。但不一定都是这样的，可能你的MdmRatio实体对应的数据库表是mdm_ratio_abc，但whatever，随便是什么，只要它真实存在就Ok)，而查询条件中的enabledNum在数据库中真正的名字是enabled_num。

这两个的作用是一样的，只是写法不同而已。涉及到HQL的知识。

Read more

  • Apr 20, 2020
  • 0 views

704. 二分查找

题目 704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
 ```

#### 提示：

你可以假设 nums 中的所有元素是不重复的。 n 将在 [1, 10000]之间。 nums 的每个元素都将在 [-9999, 9999]之间。


### 思路 二分法
```java
class Solution {
    public int search(int[] nums, int target) {
        int l = 0;
        int r = nums.length;
        while(l<r) {
            int m = l+(r-l)/2;
            if (nums[m]==target) return m;
            if (nums[m]>target) r=m;
            else l=m+1;
        }
        return -1;
    }
}

知识点 二分法

最明显的题目就是 34. Find First and Last Position of Element in Sorted Array

花花酱的二分查找专题视频：https://www.youtube.com/watch?v=v57lNF2mb_s

模板：

区间定义：[l, r) 左闭右开

其中f(m)函数代表找到了满足条件的情况，有这个条件的判断就返回对应的位置，如果没有这个条件的判断就是lowwer_bound和higher_bound.

def binary_search(l, r):
    while l < r:
        m = l + (r - l) // 2
        if f(m):    # 判断找了没有，optional
            return m
        if g(m):
            r = m   # new range [l, m)
        else:
            l = m + 1 # new range [m+1, r)
    return l    # or not found

lower bound: find index of i, such that A[i] >= x

def lowwer_bound(self, nums, target):
    # find in range [left, right)
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right - left) / 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left

upper bound : find index of i, such that A[i] > x

def higher_bound(self, nums, target):
    # find in range [left, right)
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right - left) / 2
        if nums[mid] <= target:
            left = mid + 1
        else:
            right = mid
    return left

Read more

  • Apr 19, 2020
  • 0 views

11. 盛最多水的容器

  • 难度：中等
  • 本题涉及算法：暴力 双向指针
  • 思路：暴力 双向指针
  • 类似题型：

题目 11. 盛最多水的容器

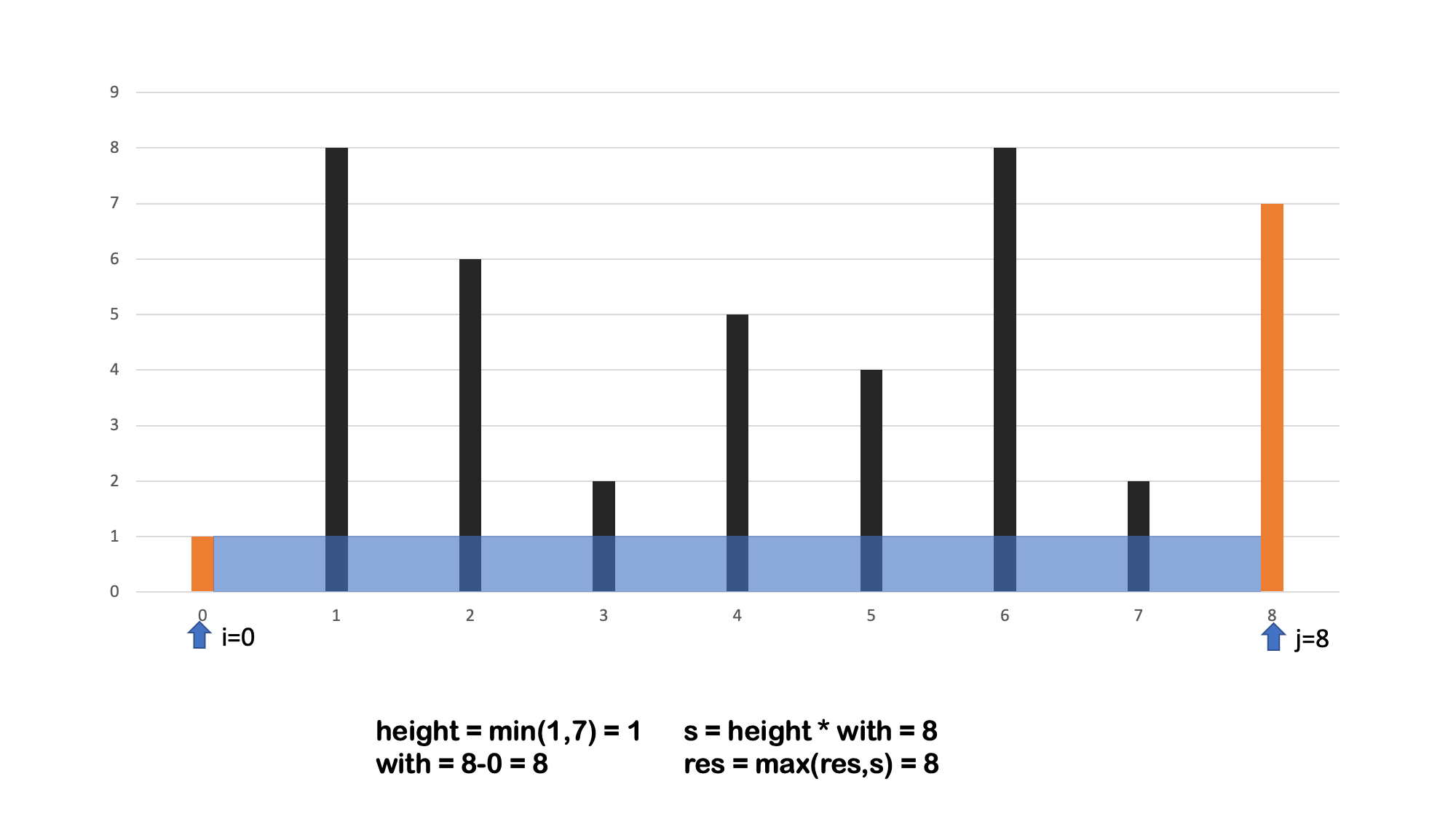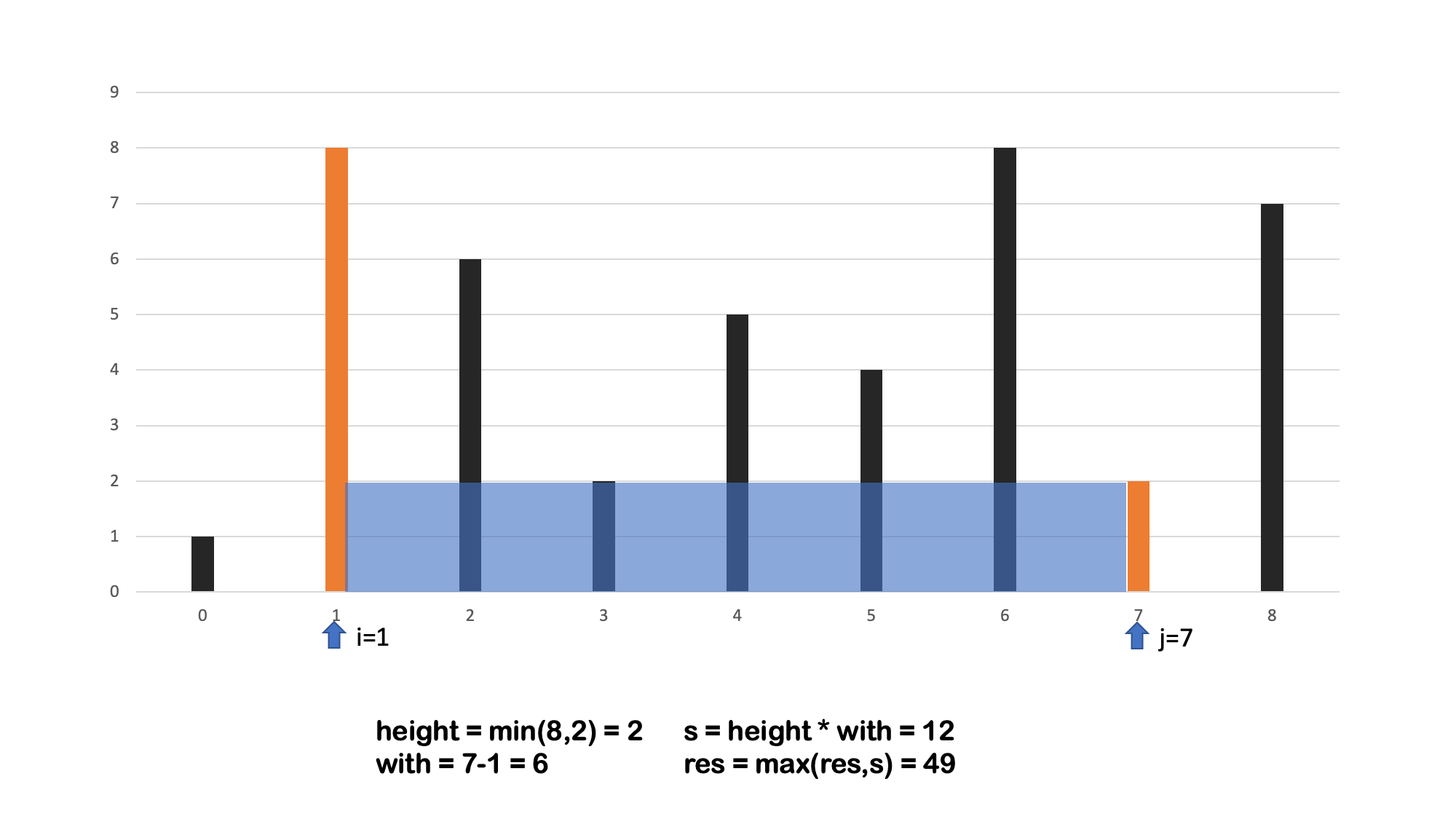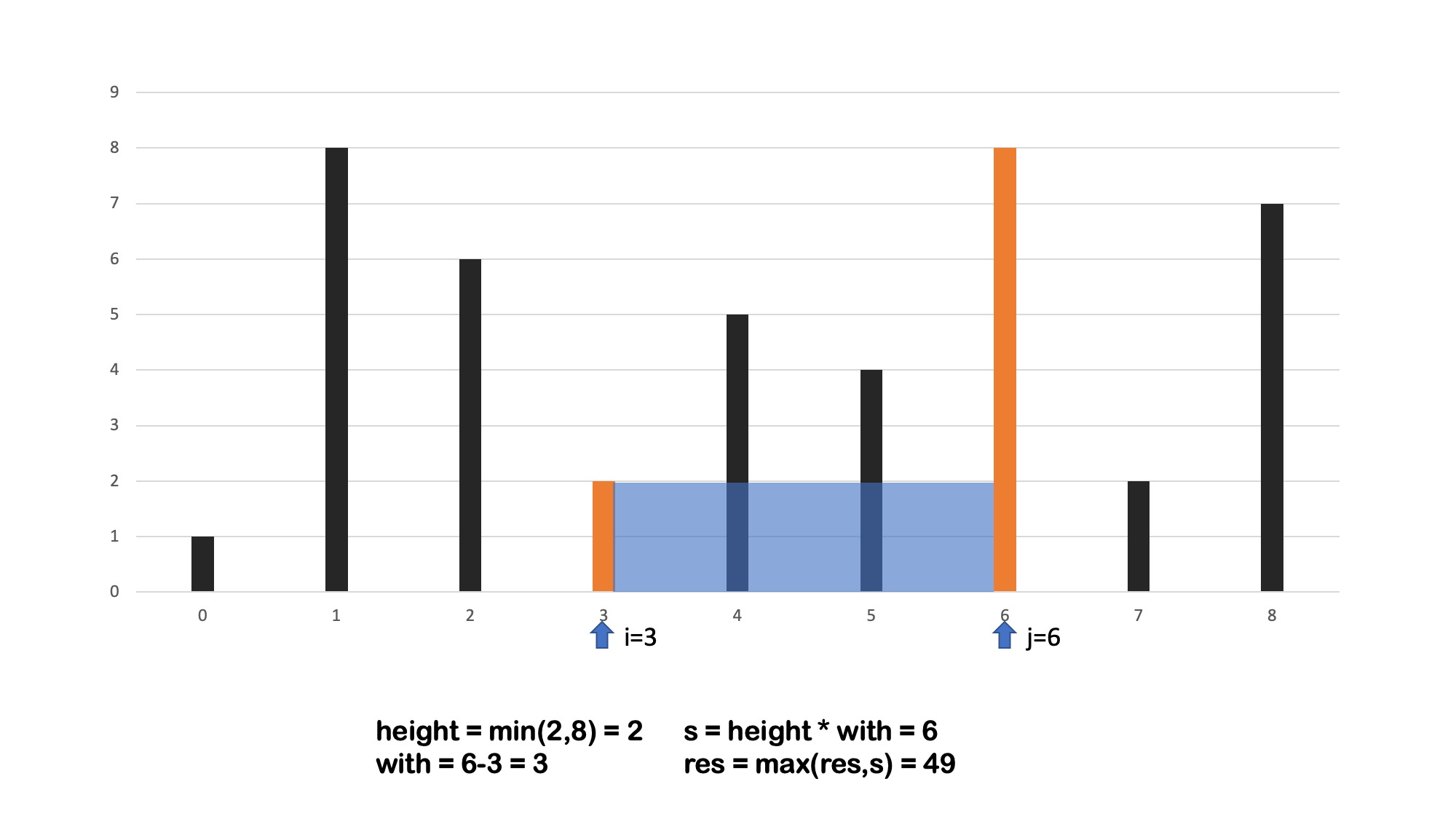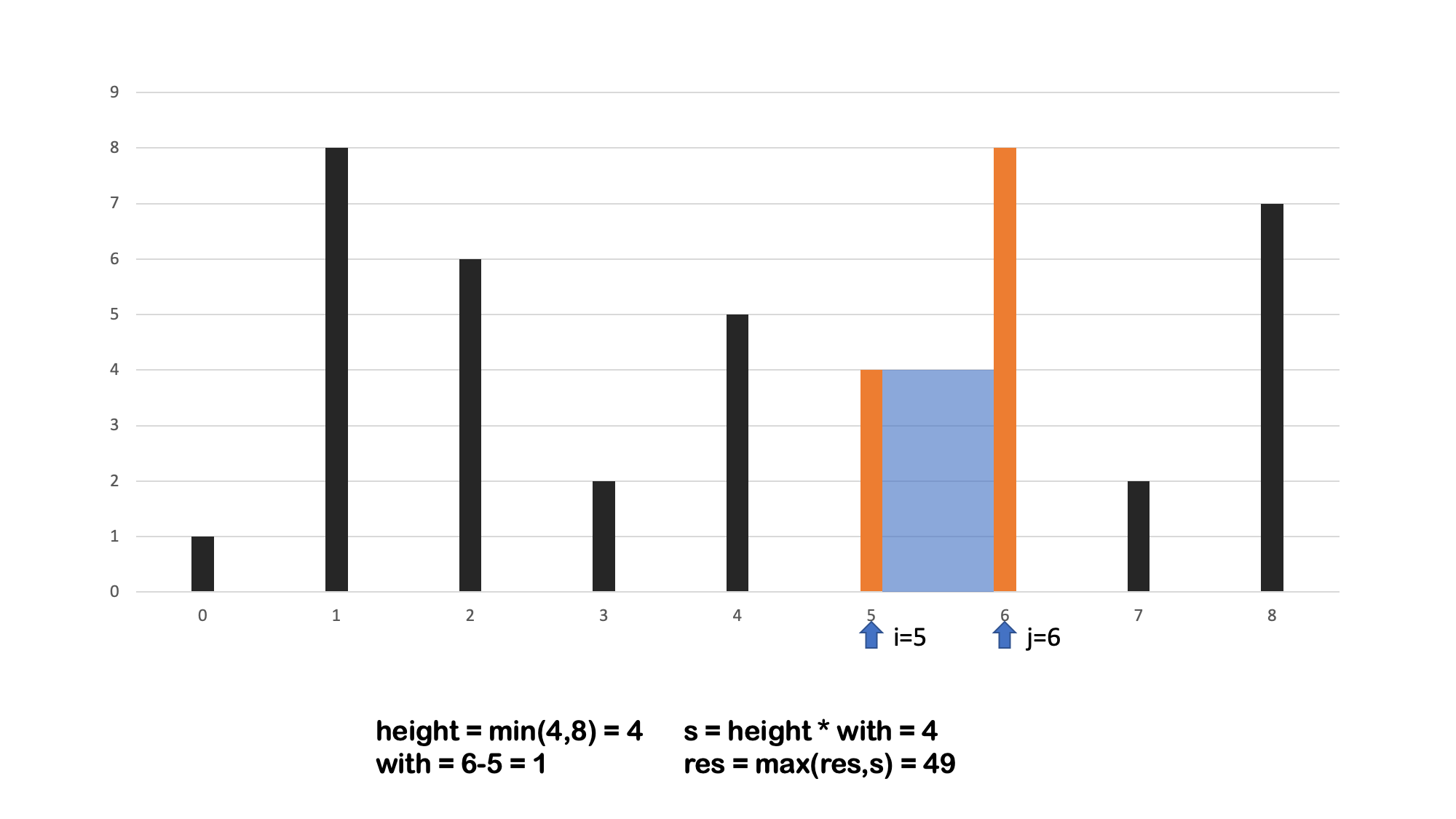
给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

pic

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例

输入：[1,8,6,2,5,4,8,3,7]
输出：49

方法一 暴力

  • 思路分析
    • 在缕思路的过程中，写一个暴力方法，不失为一直最有效的方法
  • 复杂度分析:
    • 时间复杂度 $O(N^2)$ ，N 表示数组的长度
    • 空间复杂度 $O(1)$

java

class Solution {
    public int maxArea(int[] height) {
        if (height.length<2) {
            return 0;
        }
        int max = 0;
        for (int i =0;i<height.length-1;i++) {
            for (int j=i+1;j<height.length;j++) {
                int writer = (j-i)*Math.min(height[i],height[j]);
                max = Math.max(max,writer);
            }
        }
        return max;

    }
}

方法二 双向指针

  • 算法流程： 设置双指针 i, j 分别位于容器壁两端，根据规则移动指针（后续说明），并且更新面积最大值 res，直到 i == j 时返回 res。

  • 复杂度分析：

    • 时间复杂度 $O(N)$，N 为数组的长度，双指针向中间靠拢 移动次数为 $n$ 。
    • 空间复杂度 $O(1)$，指针使用常数额外空间。

pic2

  • 可以思考下，为什么指针先移动短的一边 🤔🤔🤔🤔🤔

    java

    public class Solution {
  public int maxArea(int[] height) {
      int l = 0, r = height.length - 1;
      int ans = 0;
      while (l < r) {
          int area = Math.min(height[l], height[r]) * (r - l);
          ans = Math.max(ans, area);
          if (height[l] <= height[r]) {
              ++l;
          }
          else {
              --r;
          }
      }
      return ans;
  }
}

python

class Solution(object):
    def maxArea(self, height):
        left_index = 0
        right_index = len(height)-1
        ans = 0
        while left_index != right_index:
            left_height = height[left_index]
            right_height = height[right_index]
            product = 0
            if left_height > right_height:
                product = (right_index - left_index) * right_height
                right_index -= 1
            else:
                product = (right_index - left_index) * left_height
                left_index += 1
            ans = max(ans,product)
        return ans
  • 如果你觉得本文对你有帮助，请点赞👍支持
  • 如果有疑惑或者表达不到位的额地方 ，请在下面👇评论区指出

Read more

  • Apr 18, 2020
  • 0 views

55. 跳跃游戏

  • 难度：中等
  • 本题涉及算法：贪心 暴力回溯 递归 记忆化
  • 思路：贪心 暴力 递归 记忆化
  • 类似题型：

题目 55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

方法一 贪心算法

解题思路

  • 维护一个最远可达到的位置
  • 时间复杂度 $O(n)$ 时间复杂度 $O(1)$
class Solution:
    def canJump(self, nums: List[int]) -> bool:
        nums_len = len(nums) -1
        distance_max = 0 # 记录从0开始能到到达的最远距离
        for i in range(len(nums)):
            if i <= distance_max: # 说明 下标 i 是能涉足到
                distance_max = max(distance_max,i + nums[i]) # i 这个下标能到达的最远距离 和 distance_max 比较
                if distance_max >= nums_len:
                    return True
        return False

优化贪心算法

class Solution(object):
    def canJump(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """
        k = 0
        for i in range(len(nums)-1):
            if i > k:
                return False
            k = max(k,i+nums[i])
        return True

方法二 暴力回溯 (会超时)

解题思路

  • 从右向左推，记录能到达终点的上一个最远的距离，并记录当前的下标 作为下一个循环的目标
  • 遍历到最后 如果 i + nums[i] < p 即，flag = False,则返回 False,否则放回True
  • 时间复杂度 $O(n^2)$ 时间复杂度 $O(1)$ 
    class Solution(object):
  def canJump(self, nums):
      p = len(nums) -1
      falg = True
      while  p > 0 and falg:
          falg = False
          for i in range(p):
              if i + nums[i] >= p:
                  p = i
                  falg = True
                  break
      return falg

方法三 反向考虑，当不得不跳到0的时候，该数组才能跳不出去

解题思路

  • 可以总结出，当你不管怎么跳，都要经过0时，也就是0是你的必经之路时，是跳不出去数组的。所以只要找到一条可以跳出0 的路径，那么就可以跳跃到最后一位。
  • 那么如何判断是否能跳出0呢？设当前0的索引为index，用i遍历index-1至0，找到一个数大于index-i即可跳出0
  • 时间复杂度 $O(n^2)$ 空间复杂度 $O(1)$
public boolean canJump(int[] nums){
    for (int i=0;i<nums.length-1;i++){
        if (nums[i]==0){
            if (passZero(nums, i))
                continue;
            else
                return false;
        }
    }
    return true;
}
//判断是否能跳出当前0
public static boolean passZero(int[] nums,int index){
    for (int i=index;i>=0;i--){
        if (nums[i]>(index-i))
            return true;
    }
    return false;
}

方法四 递归

题解思路

  • 我们先通过一张来图看下递归的运作原理

1

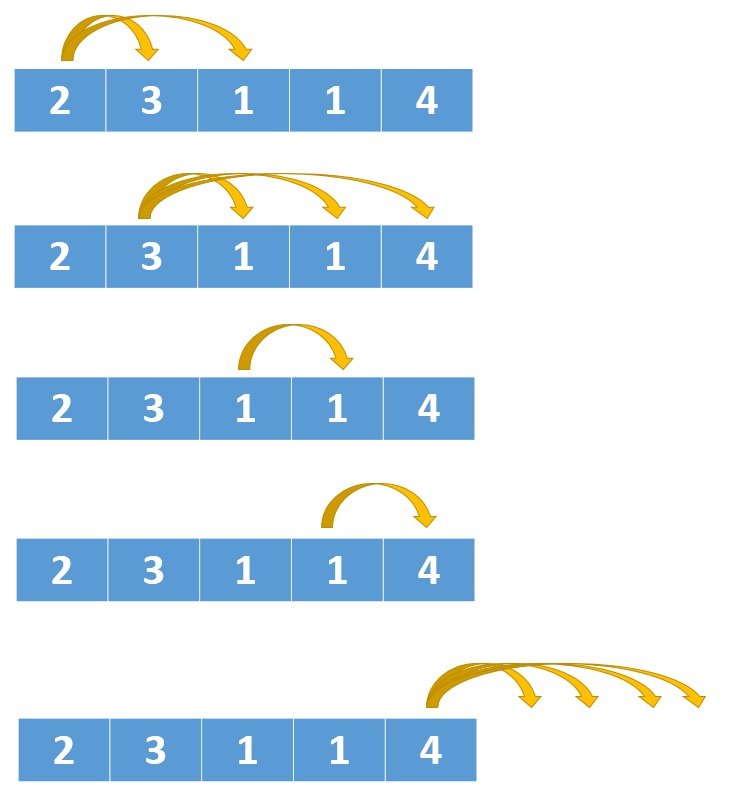
按照题目的意思 nums[0] 的值为2，所以它可以跳一步到下标1的位置，也可以跳两步到下标2的位置。 nums[1] 的值为3，所以它有三个选择，跳一步到下标2，或者跳两步到下标3，还可以跳三步到下标4。到了下标4也就到了数组的最后一个位置了，所以后面可以不用检测了，为了演示的完整性我把剩余的跳跃步骤也画出来了。 从上图中我们也可以看出，每次跳跃的步数跟数组中具体值有关，nums[1] 为3所以就有三种跳跃选择，nums[i] 为k就有k种跳跃选择。 那么大概想到这个递归实现应该是由：循环+递归组合完成的。 注意，每次跳跃的时候至少要大于等于1，否则就等于是原地打转了。

再来看下递归的执行过程:

2

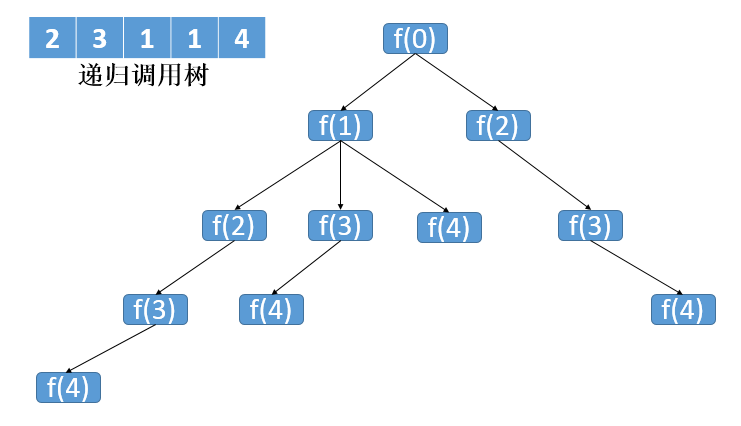
上图中f是函数名，括号里面的数字就对应了数组的下标。 数组下标1中的值是3，所以可以执行三次跳跃，对应到上图中f(1)就有三个子树。 从这里我们也可以看出，这个调用树是一棵N叉树，子节点的数量由1到N不等。 注:递归的代码执行会超时。

class Solution {
    public boolean canJump(int[] nums) {
        if(nums==null || nums.length==0) {
            return true;
        }
        return dfs(0,nums);
    }

    private boolean dfs(int index, int[] nums) {
        //递归的终止条件
        if(index>=nums.length-1) {
            return true;
        }
        //根据nums[index]表示要循环多少次，index是当前我们能到达的位置，
        //在这个基础上有 index+1，index+2.... index+i种跳跃选择
        for(int i=1;i<=nums[index];++i) {
            if(dfs(i+index,nums)) {
                return true;
            }
        }
        return false;
    }
}

方法五 递归+记忆化

  • 递归的性能差因为执行了很多重复计算

3

如上图中，f(3) 就被反复计算了好几次，既然性能不够就加缓存吧，把结果缓存起来，这样时间上可以大幅度提升。

4

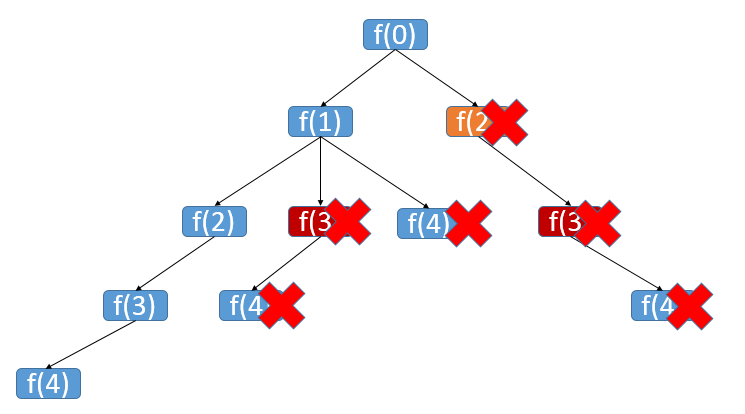
但很遗憾，即使这样优化了，还是会执行超时。

class Solution {
    public boolean canJump(int[] nums) {
        if(nums==null || nums.length==0) {
            return true;
        }
        Map<Integer,Boolean> cache = new HashMap<Integer,Boolean>();
        return dfs(0,nums,cache);
    }

    private boolean dfs(int index, int[] nums, Map<Integer,Boolean> cache) {
        if(index>=nums.length-1) {
            return true;
        }
        if(cache.containsKey(index)) {
            return cache.get(index);
        }
        for(int i=1;i<=nums[index];++i) {
            if(dfs(i+index,nums,cache)) {
                cache.put((i+index),Boolean.TRUE);
                return true;
            }
        }
        cache.put(index,Boolean.FALSE);
        return false;
    }
}

Read more

  • Apr 17, 2020
  • 0 views

Python常用命令

虚拟环境和包

创建虚拟环境

python3 -m venv tutorial-env #创建python虚拟环境
source tutorial-env/bin/activate # 在终端进入或使用phthon，可通过pycharm配置对于环境

source tutorial-env/bin/activate

使用pip管理包

pip install requests==2.6.0 # 指定版本号安装
pip install --upgrade requests # 升级最新版本包
pip show requests # 显示有关特定包的信息
pip list # 显示虚拟环境中安装的所有软件包
pip freeze > requirements.txt  # 生成一个类似的已安装包列表
pip install -r requirements.txt # 安装所有必需的包

Read more

  • 0 views

Python中 init的作用

我们经常在python的模块目录中会看到 “init.py” 这个文件，那么它到底有什么作用呢？

1. 标识该目录是一个python的模块包（module package）

如果你是使用python的相关IDE来进行开发，那么如果目录中存在该文件，该目录就会被识别为 module package 。

  1. 简化模块导入操作

    假设我们的模块包的目录结构如下：

└── mypackage
    ├── subpackage_1
    │   ├── test11.py
    │   └── test12.py
    ├── subpackage_2
    │   ├── test21.py
    │   └── test22.py
    └── subpackage_3
        ├── test31.py
        └── test32.py

　　

如果我们使用最直接的导入方式，将整个文件拷贝到工程目录下，然后直接导入：

from mypackage.subpackage_1 import test11
from mypackage.subpackage_1 import test12
from mypackage.subpackage_2 import test21
from mypackage.subpackage_2 import test22
from mypackage.subpackage_3 import test31
from mypackage.subpackage_3 import test32

当然这个例子里面文件比较少，如果模块比较大，目录比较深的话，可能自己都记不清该如何导入。（很有可能，哪怕只想导入一个模块都要在目录中找很久）

这种情况下，init.py 就很有作用了。我们先来看看该文件是如何工作的。

2.1 init.py 是怎么工作的？

实际上，如果目录中包含了 init.py 时，当用 import 导入该目录时，会执行 init.py 里面的代码。

我们在mypackage目录下增加一个 init.py 文件来做一个实验：

└── mypackage
    ├── __init__.py
    ├── subpackage_1
    │   ├── test11.py
    │   └── test12.py
    ├── subpackage_2
    │   ├── test21.py
    │   └── test22.py
    └── subpackage_3
        ├── test31.py
        └── test32.py

mypackage/init.py 里面加一个print，如果执行了该文件就会输出：

print("You have imported mypackage")

下面直接用交互模式进行 import

>>> import mypackage
You have imported mypackage

很显然，init.py 在包被导入时会被执行。

2.2 控制模块导入

我们再做一个实验，在 mypackage/init.py 添加以下语句：

from subpackage_1 import test11

我们导入 mypackage 试试:

>>> import mypackage
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/home/taopeng/Workspace/Test/mypackage/__init__.py", line 2, in <module>
    from subpackage_1 import test11
ImportError: No module named 'subpackage_1'

报错了。。。怎么回事？

原来，在我们执行import时，当前目录是不会变的（就算是执行子目录的文件），还是需要完整的包名。

from mypackage.subpackage_1 import test11

综上，我们可以在__init__.py 指定默认需要导入的模块　　

2.3 偷懒的导入方法

有时候我们在做导入时会偷懒，将包中的所有内容导入

from mypackage import *

这是怎么实现的呢？ all 变量就是干这个工作的。

all 关联了一个模块列表，当执行 from xx import * 时，就会导入列表中的模块。我们将 init.py 修改为 。

__all__ = ['subpackage_1', 'subpackage_2']

这里没有包含 subpackage_3，是为了证明 all 起作用了，而不是导入了所有子目录。

>>> from mypackage import *
>>> dir()
['__builtins__', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'subpackage_1', 'subpackage_2']
>>>
>>> dir(subpackage_1)
['__doc__', '__loader__', '__name__', '__package__', '__path__', '__spec__']

子目录的中的模块没有导入！！！

该例子中的导入等价于

from mypackage import subpackage_1, subpackage_2

因此，导入操作会继续查找 subpackage_1 和 subpackage_2 中的 init.py 并执行。（但是此时不会执行 import * ）

我们在 subpackage_1 下添加 init.py 文件:

__all__ = ['test11', 'test12']

# 默认只导入test11
from mypackage.subpackage_1 import test11

再来导入试试

>>> from mypackage import *
>>> dir()
['__builtins__', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'subpackage_1', 'subpackage_2']
>>>
>>> dir(subpackage_1)
['__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', 'test11']

如果想要导入子包的所有模块，则需要更精确指定。

>>> from mypackage.subpackage_1 import *
>>> dir()
['__builtins__', '__doc__', '__loader__', '__name__', '__package__', '__spec__', 'test11', 'test12']

3. 配置模块的初始化操作

在了解了 init.py 的工作原理后，应该能理解该文件就是一个正常的python代码文件。

因此可以将初始化代码放入该文件中。

Read more

  • 0 views

56. 合并区间

  • 难度：中等
  • 本题涉及算法：贪心
  • 思路：贪心
  • 类似题型：

题目 56. 合并区间

给出一个区间的集合，请合并所有重叠的区间。

示例

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

方法一 贪心

解题思路

  • 当前下标和结果集中 最后一个数组的末尾元素进行比较(在错误的思维中，总会出现当前数组和下一个数组的比较)
  • 按照左端点升序排序，然后遍历。
    • 如果当前遍历到的区间的左端点 > 结果集中最后一个区间的右端点，说明它们没有交集，此时把区间添加到结果集；
    • 如果当前遍历到的区间的左端点 <= 结果集中最后一个区间的右端点，说明它们有交集，此时产生合并操作，即：对结果集中最后一个区间的右端点更新（取两个区间的最大值）。

python

class Solution(object):
    def merge(self, intervals):
        if not intervals:
            return []
        intervals.sort() # 按照起点排序
        ans = [intervals[0]] #
        for i in range(1,len(intervals)):
            if intervals[i][0]<=ans[-1][1]:
                if intervals[i][1]<=ans[-1][1]:
                    ans[-1][1] = ans[-1][1]
                else:
                    ans[-1][1] = intervals[i][1]
            else:
                ans.append(intervals[i])
        return ans

优化版

class Solution(object):
    def merge(self, intervals):
        if not intervals:
            return []
        intervals.sort() # 按照起点排序
        ans = [intervals[0]] #
        for i in range(1,len(intervals)):
            if intervals[i][0]<=ans[-1][1]:
                ans[-1][1] = max(ans[-1][1],intervals[i][1])
                # if intervals[i][1]<=ans[-1][1]:
                #     ans[-1][1] = ans[-1][1]
                # else:
                #     ans[-1][1] = intervals[i][1]
            else:
                ans.append(intervals[i])
        return ans

java

int len = intervals.length;
        if (len < 2) {
            return intervals;
        }
        // 按照起点排序
        Arrays.sort(intervals, Comparator.comparingInt(o -> o[0]));

        List<int[]> res = new ArrayList();
        res.add(intervals[0]);
        for (int i = 1; i < len; i++) {
            int[] curInterval = intervals[i];
            // 每次新遍历到的列表与当前结果集中的最后一个区间的末尾端点进行比较
            int[] peek = res.get(res.size() - 1);

            if (curInterval[0] > peek[1]) {
                res.add(curInterval);
            } else {
                // 注意，这里应该取最大
                peek[1] = Math.max(curInterval[1], peek[1]);
            }
        }
        return res.toArray(new int[res.size()][]);

方法二

解题思路

2 个区间的关系有以下 6 种，但是其实可以变成上面 3 种情况（只需要假设 第一个区间的起始位置 ≤ 第二个区间的起始位置，如果不满足这个假设，交换这两个区间）。这 3 种情况的合并的逻辑都很好写。

pic1

class Solution {
    public int[][] merge(int[][] intervals) {
        // 先按照区间起始位置排序
        Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
        // 遍历区间
        int[][] res = new int[intervals.length][2];
        int idx = -1;
        for (int[] interval: intervals) {
            // 如果结果数组是空的，或者当前区间的起始位置 > 结果数组中最后区间的终止位置，
            // 则不合并，直接将当前区间加入结果数组。
            if (idx == -1 || interval[0] > res[idx][1]) {
                res[++idx] = interval;
            } else {
                // 反之将当前区间合并至结果数组的最后区间
                res[idx][1] = Math.max(res[idx][1], interval[1]);
            }
        }
        return Arrays.copyOf(res, idx + 1);
    }
}

知识点

Read more

  • Apr 16, 2020
  • 0 views
Search