- 难度:
中等 - 本题涉及算法:
贪心暴力回溯递归记忆化 - 思路:
贪心暴力递归记忆化 - 类似题型:
题目 55. 跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
方法一 贪心算法
解题思路
- 维护一个最远可达到的位置
- 时间复杂度 $O(n)$ 时间复杂度 $O(1)$
class Solution:
def canJump(self, nums: List[int]) -> bool:
nums_len = len(nums) -1
distance_max = 0 # 记录从0开始能到到达的最远距离
for i in range(len(nums)):
if i <= distance_max: # 说明 下标 i 是能涉足到
distance_max = max(distance_max,i + nums[i]) # i 这个下标能到达的最远距离 和 distance_max 比较
if distance_max >= nums_len:
return True
return False
优化贪心算法
class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
k = 0
for i in range(len(nums)-1):
if i > k:
return False
k = max(k,i+nums[i])
return True
方法二 暴力回溯 (会超时)
解题思路
- 从右向左推,记录能到达终点的上一个最远的距离,并记录当前的下标 作为下一个循环的目标
- 遍历到最后 如果
i + nums[i] < p即,flag = False,则返回False,否则放回True - 时间复杂度 $O(n^2)$ 时间复杂度 $O(1)$
class Solution(object): def canJump(self, nums): p = len(nums) -1 falg = True while p > 0 and falg: falg = False for i in range(p): if i + nums[i] >= p: p = i falg = True break return falg
方法三 反向考虑,当不得不跳到0的时候,该数组才能跳不出去
解题思路
- 可以总结出,当你不管怎么跳,都要经过0时,也就是0是你的必经之路时,是跳不出去数组的。所以只要找到一条可以跳出0 的路径,那么就可以跳跃到最后一位。
- 那么如何判断是否能跳出0呢?设当前0的索引为index,用i遍历index-1至0,找到一个数大于index-i即可跳出0
- 时间复杂度 $O(n^2)$ 空间复杂度 $O(1)$
public boolean canJump(int[] nums){
for (int i=0;i<nums.length-1;i++){
if (nums[i]==0){
if (passZero(nums, i))
continue;
else
return false;
}
}
return true;
}
//判断是否能跳出当前0
public static boolean passZero(int[] nums,int index){
for (int i=index;i>=0;i--){
if (nums[i]>(index-i))
return true;
}
return false;
}
方法四 递归
题解思路
- 我们先通过一张来图看下递归的运作原理
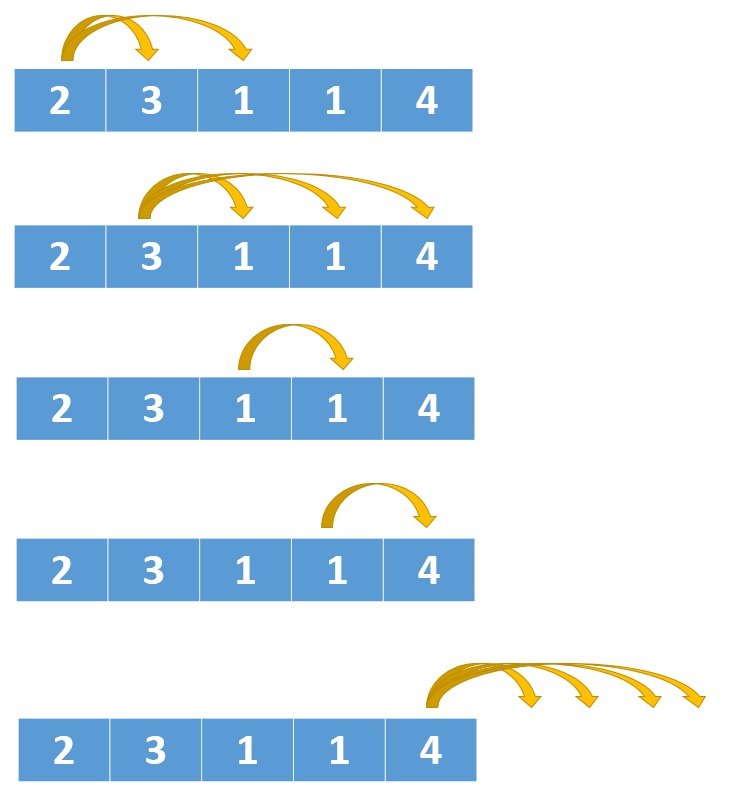
按照题目的意思 nums[0] 的值为2,所以它可以跳一步到下标1的位置,也可以跳两步到下标2的位置。
nums[1] 的值为3,所以它有三个选择,跳一步到下标2,或者跳两步到下标3,还可以跳三步到下标4。到了下标4也就到了数组的最后一个位置了,所以后面可以不用检测了,为了演示的完整性我把剩余的跳跃步骤也画出来了。
从上图中我们也可以看出,每次跳跃的步数跟数组中具体值有关,nums[1] 为3所以就有三种跳跃选择,nums[i] 为k就有k种跳跃选择。
那么大概想到这个递归实现应该是由:循环+递归组合完成的。
注意,每次跳跃的时候至少要大于等于1,否则就等于是原地打转了。
再来看下递归的执行过程:
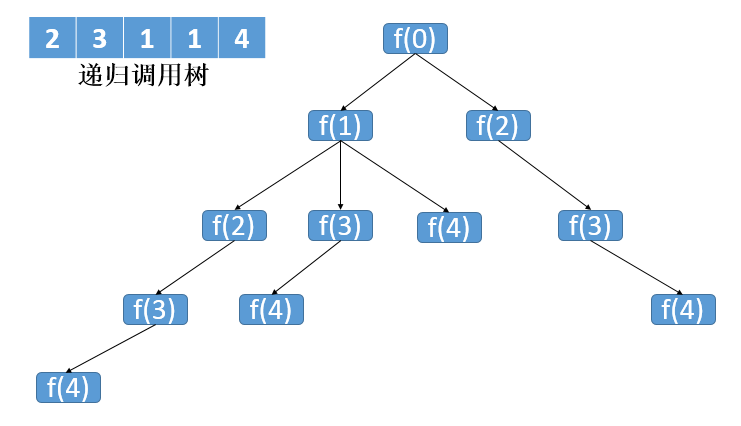
上图中f是函数名,括号里面的数字就对应了数组的下标。 数组下标1中的值是3,所以可以执行三次跳跃,对应到上图中f(1)就有三个子树。 从这里我们也可以看出,这个调用树是一棵N叉树,子节点的数量由1到N不等。 注:递归的代码执行会超时。
class Solution {
public boolean canJump(int[] nums) {
if(nums==null || nums.length==0) {
return true;
}
return dfs(0,nums);
}
private boolean dfs(int index, int[] nums) {
//递归的终止条件
if(index>=nums.length-1) {
return true;
}
//根据nums[index]表示要循环多少次,index是当前我们能到达的位置,
//在这个基础上有 index+1,index+2.... index+i种跳跃选择
for(int i=1;i<=nums[index];++i) {
if(dfs(i+index,nums)) {
return true;
}
}
return false;
}
}
方法五 递归+记忆化
- 递归的性能差因为执行了很多重复计算

如上图中,f(3) 就被反复计算了好几次,既然性能不够就加缓存吧,把结果缓存起来,这样时间上可以大幅度提升。
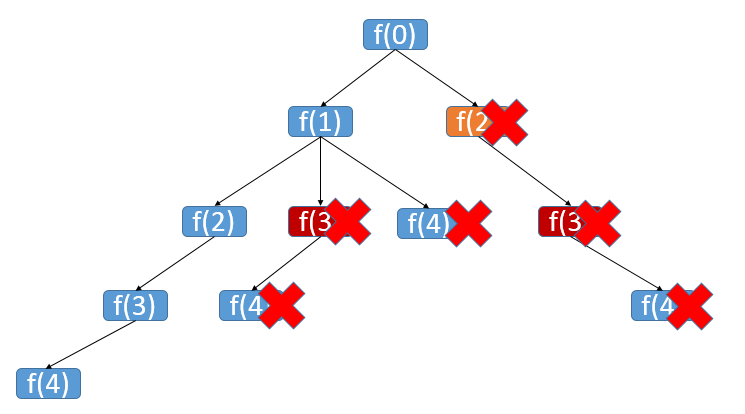
但很遗憾,即使这样优化了,还是会执行超时。
class Solution {
public boolean canJump(int[] nums) {
if(nums==null || nums.length==0) {
return true;
}
Map<Integer,Boolean> cache = new HashMap<Integer,Boolean>();
return dfs(0,nums,cache);
}
private boolean dfs(int index, int[] nums, Map<Integer,Boolean> cache) {
if(index>=nums.length-1) {
return true;
}
if(cache.containsKey(index)) {
return cache.get(index);
}
for(int i=1;i<=nums[index];++i) {
if(dfs(i+index,nums,cache)) {
cache.put((i+index),Boolean.TRUE);
return true;
}
}
cache.put(index,Boolean.FALSE);
return false;
}
}