JAVA 牛牛

Home

面试题56 - I. 数组中数字出现的次数

题目 面试题56 - I. 数组中数字出现的次数

一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。

示例

示例 1：

输入：nums = [4,1,4,6]
输出：[1,6] 或 [6,1]

示例 2：

输入：nums = [1,2,10,4,1,4,3,3]
输出：[2,10] 或 [10,2]

限制：

2 <= nums <= 10000

方法二 二分法

  • 知识提供一种思路，这个代码在leetcode 运行会超时
  • 一个很棒的概念 只要符合单调，就可以二分
class Solution {
    public int[] singleNumbers(int[] nums) {
        int sum =0 ,min=Integer.MAX_VALUE, max = Integer.MIN_VALUE,zeroCount = 0;
        for (int num:nums) {
            if (num==0)
                zeroCount += 1;
            min = Math.min(min,num);
            max = Math.max(max,num);
            sum ^= num;
        }
        // 需要特判一下某个数是0的情况。
        if (zeroCount == 1)
            return new int[]{sum,0};
        int lo =min,hi = max;
        while (lo<=hi) {
            int mid = lo<0?lo+hi >>1 :lo+(hi-lo)>>1;
            int loSum =0,hiSum = 0;
            for (int num:nums) {
                if (num<=mid)
                    loSum ^= num;
                else
                    hiSum ^= num;
            }

            if (loSum!=0&&hiSum!=0)
                // 两个都不为0，说明 p 和 q 分别落到2个数组里了。
                return new int[]{loSum,hiSum};

            if (loSum==0)
                // 说明 p 和 q 都比 mid 大，所以比 mid 小的数的异或和变为0了。
                lo =mid;
            else
                // 说明 p 和 q 都不超过 mid
                hi = mid;

        }
        // 其实如果输入是符合要求的，程序不会执行到这里，为了防止compile error加一下
        return null;
    }
}

解题思路 分组异或 (需要对位运算符理解很深刻)

class Solution(object):
    def singleNumbers(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        ret = functools.reduce(lambda x, y: x ^ y, nums) # 运算规则：0^0=0；   0^1=1；   1^0=1；   1^1=0；
        # 获得ret中最低位的1 0&0=0;   0&1=0;    1&0=0;     1&1=1;
        div = 1
        while div & ret == 0:
            div <<= 1
        a, b = 0, 0
        for n in nums:
            if n & div:
                a ^= n
            else:
                b ^= n
        return [a, b]

Read more

  • Apr 28, 2020
  • 0 views

136. 只出现一次的数字

题目 136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

方法一 数组

解题思路

  • 题目说 其余每个元素均出现两次，那么当元素第一次出现，则添加到数组，再次出现则删除该元素
  • 除了某个元素只出现一次以外，那么剩下的最后一个元素 就是题解
def singleNumber(nums):
    no_duplicate_list = []
    for num in nums:
        if num not in no_duplicate_list:
            no_duplicate_list.append(num)
        else:
            no_duplicate_list.remove(num)
    return no_duplicate_list.pop() # 在 数组中取出该数字

复杂度分析

  • 时间复杂度度：$O(n)$ 如果当前数组的长度为 $n$ ，则每个元素遍历一遍，则为 $n$
  • 空间复杂度度：$O(n/2+1)$ ，如果当前数组 前 $n/2+1$ 个元素为不同元素，则最长需保存 $n/2+1$ 个元素

方法二 位运算

解题思路

  • 交换律： $p⊕q=q⊕p$
  • 结合律： $p⊕(q⊕r)=(p⊕q)⊕r$
  • 恒等率： $p⊕0=p$
  • 归零率： $p⊕p=0$

代码

java

class Solution {
    public int singleNumber(int[] nums) {
        int sum = 0;
        for(int i=0;i<nums.length;i++) {
            sum ^= nums[i]; // 异或
        }
        return sum;

    }
}

python

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        sum = 0
        for num in nums:
            sum ^= num
        return sum

复杂度分析

  • 时间复杂度度：$O(n)$ 如果当前数组的长度为 $n$ ，则每个元素遍历一遍，则为 $n$
  • 空间复杂度度：$O(1)$
  • 如果你觉得本文对你有帮助，请点赞👍支持
  • 如果有疑惑或者表达不到位的额地方 ，请在下面👇评论区指出

Read more

  • Apr 28, 2020
  • 0 views

81. 搜索旋转排序数组 II

题目 81. 搜索旋转排序数组 II

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。

编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

示例

示例 1:

输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true

示例 2:

输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false

进阶:

这是 搜索旋转排序数组 的延伸题目，本题中的 nums  可能包含重复元素。
这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

类似题型 33. 搜索旋转排序数组

解题思路

  • 被旋转的值肯定小于 nums[0]
  • 注意对 [1,3,1,1,1]做特殊处理

代码

class Solution {
    public boolean search(int[] nums, int target) {
        int left = 0;
        int right = nums.length -1;
        while (left<=right) { // 有些字段会重复出现，所以需要 <=
            int mid = left + ((right-left)>>1);
            if(nums[mid]==target)
                return true;
            if (nums[left] == nums[mid] && nums[mid] == nums[right]) { // 对数组如 [1,3,1,1,1]做特殊处理
                left++;
                right--;
            }else if (nums[mid]>=nums[left]) {// mid的左半部分升序
                if (target>=nums[left]&&target<nums[mid])
                    right = mid -1;
                else
                    left = mid + 1;
            } else {
                if (target<=nums[right]&&target>nums[mid])
                    left = mid +1;
                else
                    right = mid-1;
            }
        }

        return false;
    }
}

Read more

  • Apr 27, 2020
  • 0 views

33. 搜索旋转排序数组

题目 33. 搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

解题思路

  • 被旋转的值肯定小于 nums[0]

解题思路一 直接对旋转数组进行二分查找。

题目要求 O(logN) 的时间复杂度，基本可以断定本题是需要使用二分查找，怎么分是关键。
由于题目说数字了无重复，举个例子：
1 2 3 4 5 6 7 可以大致分为两类，
第一类 2 3 4 5 6 7 1 这种，也就是 nums[left] <= nums[mid]。此例子中就是 2 <= 5。
这种情况下，前半部分有序。因此如果 nums[left] <=target<nums[mid]，则在前半部分找，否则去后半部分找。
第二类 6 7 1 2 3 4 5 这种，也就是 nums[left] > nums[mid]。此例子中就是 6 > 2。
这种情况下，后半部分有序。因此如果 nums[mid] <target<=nums[right]，则在后半部分找，否则去前半部分找。

class Solution {
    public int search(int[] nums, int target) {
        if (nums==null||nums.length==0) {
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target)
                return mid;
            if (nums[left] <= nums[mid]) {// mid的左半部分升序
                if (target < nums[mid] && target >= nums[left])
                    right = mid - 1;
                else
                    left = mid + 1;
            } else {
                if (target > nums[mid] && target <= nums[right])
                    left = mid + 1;
                else
                    right = mid - 1;
            }
        }
        return -1;
    }
}

解题思路二 将「旋转数组查找目标值」 转化成 「有序数组查找目标值」

对于旋转数组 nums = [4,5,6,7,0,1,2] 首先根据 nums[0] 与 target 的关系判断 target 是在左段还是右段。

  • 例如 target = 5, 目标值在左半段，因此在 [4, 5, 6, 7, inf, inf, inf] 这个有序数组里找就行了；
  • 例如 target = 1, 目标值在右半段，因此在 [-inf, -inf, -inf, -inf, 0, 1, 2] 这个有序数组里找就行了。
class Solution {
    public int search(int[] nums, int target) {
        int lo = 0, hi = nums.length - 1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            // 先根据 nums[0] 与 target 的关系判断目标值是在左半段还是右半段
            if (target >= nums[0]) {
                // 目标值在左半段时，若 mid 在右半段，则将 mid 索引的值改成 inf
                if (nums[mid] < nums[0]) {
                    nums[mid] = Integer.MAX_VALUE;
                }
            } else {
                // 目标值在右半段时，若 mid 在左半段，则将 mid 索引的值改成 -inf
                if (nums[mid] >= nums[0]) {
                    nums[mid] = Integer.MIN_VALUE;
                }
            }

            if (nums[mid] < target) {
                lo = mid + 1;
            } else {
                hi = mid - 1;
            }
        }
        return -1;
    }
}

Read more

  • Apr 27, 2020
  • 0 views

动态规范(dp)

类似题型

文案

动态规范总体思想

  1. 基于 斐波那契数列
\[fib(n)=\begin{cases} 1 & n=1 或 n=2 \\ fib(n-1) + fib(n-2) & o/w \\ \end{cases}\]
  1. 动态规划解决来递归的重复子问题，递归空间时间复杂度 $O(n^2)$ ,动态规划 $O(n)$
    • 比如说 下面的 例题二 中通过数组保存过程状态，需要用的时候直接获取到，不需要在算一遍

pic0

做题思路

  • 寻找子问题
  • 选择第 i 个数字
  • 不选 第 i 个数字
  • 找出口

例题一

在数组中找出数字和最大的数，其中两个数不能是相邻的两个数

示例

arr = [1,2,4,1,7,8,3]
返回最大数为 15 [1,4,8]

方法一 动态规划

解题思路

  • 如图 思路分析
    1. 先为数组添加下标 方便理解
    2. 根据条件可知 只能找不相邻的两个数
    3. 假设 opt[i] 表示到下标为 i 的最佳方案
    4. 选择下标为 i 的方案 opt[i-2] + arr[i]
    5. 不选择下标为 i 的方案 opt[i-1]
    6. 再比较 这两个的大小
    7. 找出口
      • 当数组 arr 只有一个数字的时候 最大数 opt[0] = arr[0]
      • 当数组 arr 有两个数字的时候 最大数 opt[1] = max(arr[0],arr[1])
  • 根据思路可推到出公式
\[opt(i)=\begin{cases} arr[0] & i = 0 \\ max(arr[0],arr[1]) & i = 1 \\ \end{cases}\] \[opt(i)=max=\begin{cases} opt[i-2]+ arr[i] & 选择 \\ opt[i-1] & 不选 \\ \end{cases}\]

pic1

pic2

动态规划写法

python
class Solution:
    def massage(self, nums: List[int]) -> int:
        lenNums = len(nums)
        if nums == None or lenNums ==0:
            return 0
        opt = [0] * lenNums
        if lenNums == 1:
            return nums[0]
        if lenNums == 2:
            return max(nums[0],nums[1])
        opt[0] = nums[0]
        opt[1] = max(nums[0],nums[1])
        for i in range(2,lenNums):
            a = opt[i-2] + nums[i]
            b = opt[i-1]
            opt[i] = max(a,b)
        return opt[lenNums-1]
java
public class Solution {

    public int massage(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        if (len == 1) {
            return nums[0];
        }
        int[] opt = new int[len];
        opt[0] = nums[0];
        opt[1] = Math.max(nums[0],nums[1]);
        for(int i = 2;i<len;i++) {
            int a = opt[i-2] + nums[i];
            int b = opt[i-1];
            opt[i] = Math.max(a,b);
        }
        return opt[len-1];
    }
}

递归写法

  • 需要把 arr 传递进去 
    def rec_opt(arr,i):
  # 找出口
  if i ==0:
      return arr[0]
  elif i==1:
      return max(arr[0],arr[1])
  else:
      a = rec_opt(arr,i-2) + arr[i] #选择arr[i]
      b = rec_opt(arr,i-1)# 不选arr[i]
      return max(a,b)

例题二

在数组中找出和为s的数，有则返回 True，没有则返回 False

示例

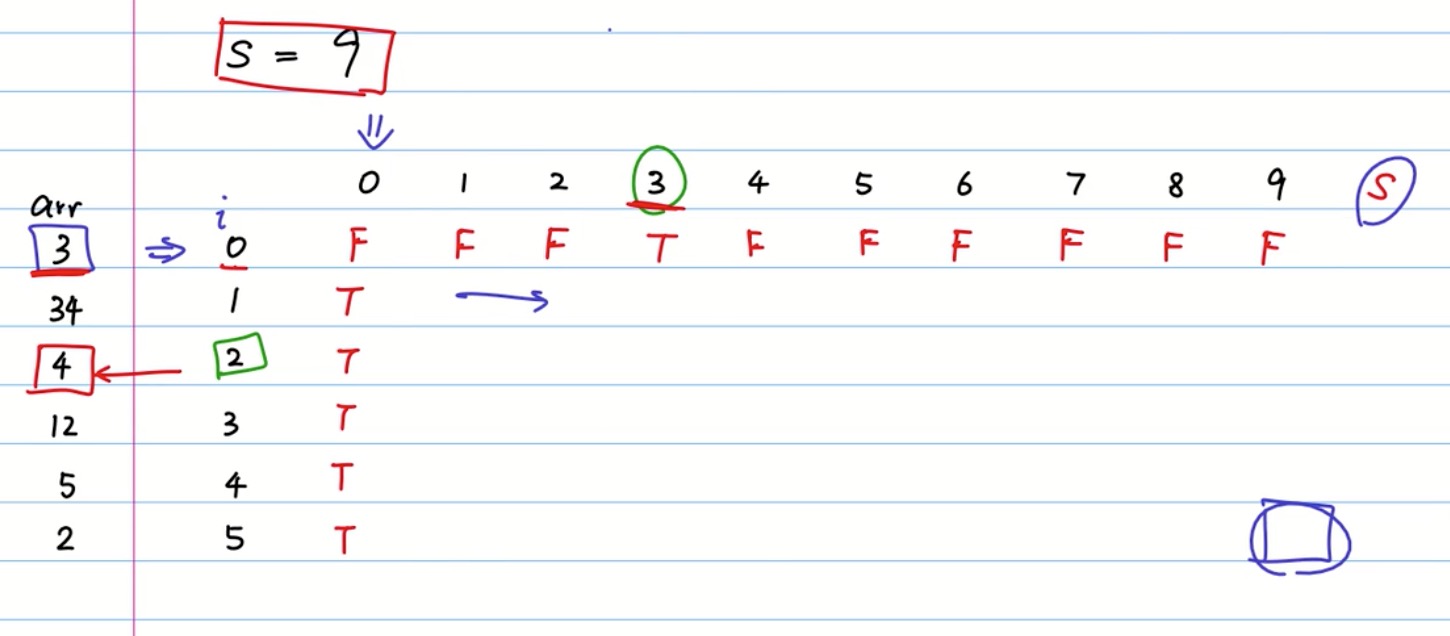
arr = [3,34,4,12,5,2]
k = 9
结果 为True (4+5=9)

方法一 动态规划

解题思路

  • 如图 思路分析
    1. 先为数组添加下标 方便理解
    2. 根据条件可知 需要找出和为 s 的数
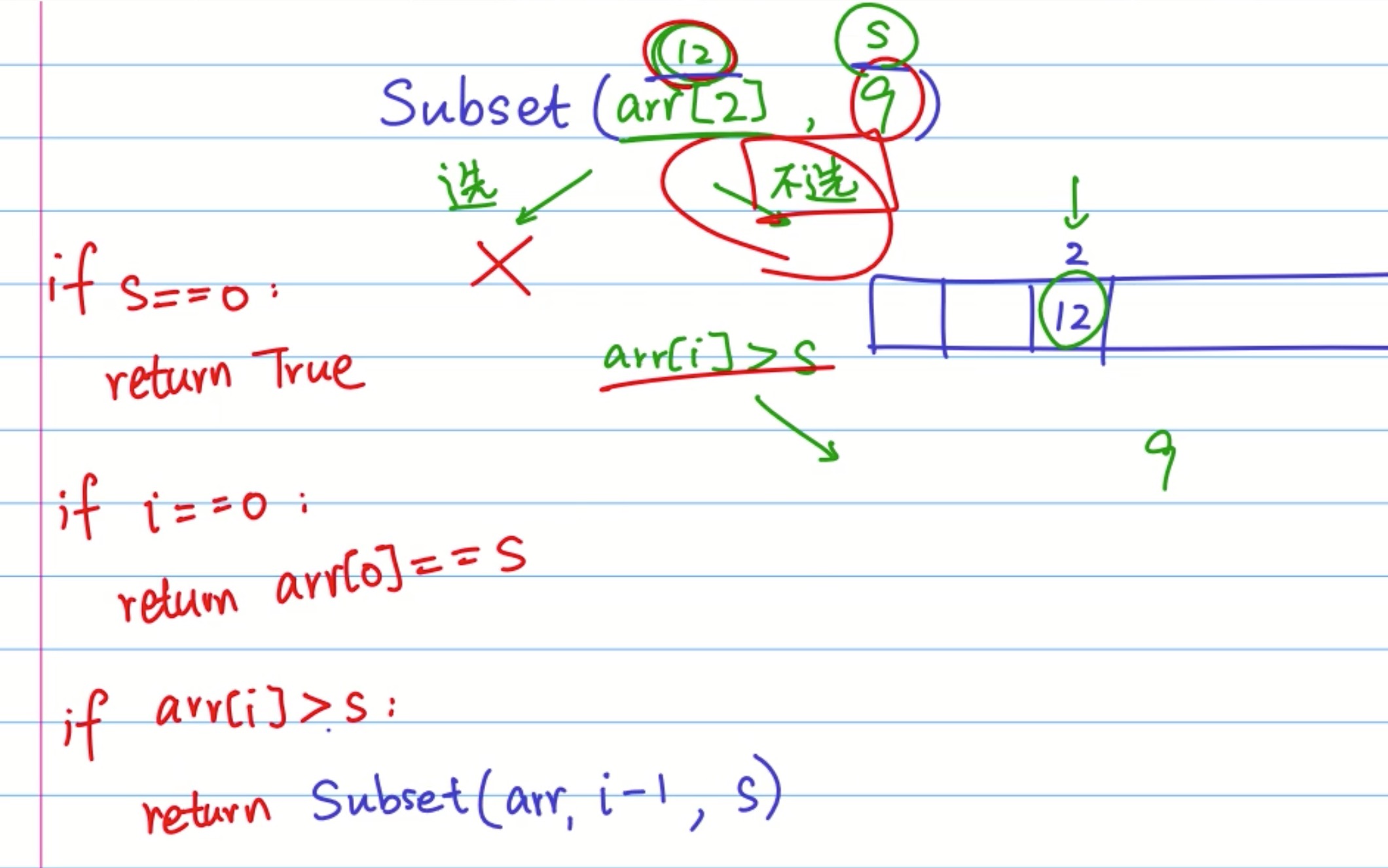
    3. 我们假设 subset(i,s) i 表示数组下标 s 表示需要求的数
    4. opt[i] 表示到下标为 i 的最佳方案
    5. 选择下标为 i 的方案 那么剩下的数组需要 subset(arr[i-1],s-arr[i])
    6. 不选择下标为 i 的方案 那么剩下的数组需要 subset[i-1] + arr[i]
    7. 在比较 这两个的大小
    8. 找出口
      • 当 s = 0 表示 i 之前的数字加起来已经等于 s 了 则直接返回 True
      • 当 i = 0 的时候，表示 arr[0] == s 才能返回为 True
      • 当左边的数字比右边的 s 还有大，则(s-arr[i]<0) ,所以只能选择第二种情况，subset[i-1] + arr[i]
  • 根据思路可推到出公式
\[subset(i,s)=\begin{cases} return True & s==0 \\ arr[0]==s & i==0 \\ subset(i-1,s) & arr[i]>s \\ subset(i-1,s-arr[i]) & arr[i]<s 且 选择 i \\ subset(i-1,s) & arr[i]<s 不选择 i\\ \end{cases}\]

pic3

pic4

pic5

动态规划写法

  • 需要使用二维数组来保存中间所有的动态过程
  • 通常使用二维数组 ，都会把二维数组的下标分别加 1
  • 返回 二维数组的最后一个数组 
    import numpy as np
def dp_subset(arr,S):
  subset = np.zeros((len(arr),S+1),dtype = bool)
  subset[:,0] = True
  subset[0,:] = False
  subset[0,arr[0]] = True
  for i in range(1,len(arr)):
      for s in range(1,S+1):
          if arr[i]>s:
              subset[i,s] = subset[i-1,s]
          else:
              a = subset[i-1,s-arr[i]] #选择arr[i]
              b = subset[i-1,s] # 不选arr[i]
              subset[i,s] = a or b
  r ,c = subset.shape
  return subset[r-1,c-1]

递归写法

  • 需要把 arr 传递进去 
    arr = [3,34,4,12,5,2]
# 递归写法
def rec_subset(arr,i,s):
  # 找出口
  if s ==0:
      return True
  if i ==0:
      return arr[0]==s
  if arr[i]>s:
      return rec_subset(arr,i-1,s)
  else:
      a = rec_subset(arr,i-1,s-arr[i]) #选择arr[i]
      b = rec_subset(arr,i-1,s) # 不选arr[i]
      return a or b

参考视频

Read more

  • Apr 27, 2020
  • 0 views

面试题 08.11. 硬币

  • 难度：中等
  • 本题涉及算法：动态规划(dp)
  • 思路：完全背包问题

题目 面试题 08.11. 硬币

硬币。给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。(结果可能会很大，你需要将结果模上1000000007)

示例

示例1:

输入: n = 5
输出：2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1

示例2:

输入: n = 10
输出：4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1
说明：

注意:

你可以假设：

0 <= n (总金额) <= 1000000

解题思路

由于无限数量硬币的选择，应该是一个完全背包问题

  • dp 数组建立：dp[i][j] 表示 i 种硬币组成面值为 j 时的方法数

  • 考虑 base case

    • dp[0][j] 0 种硬币组成面值 j，不可能有方案，因此是 0， java 初始化时数组是 0，不用特殊处理

    • dp[i][0] 多种硬币组成面值 0，只有一种方案，就是一枚也不选

  • 状态转移方程：

    • dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i])

    • 其中 dp[i - 1][j] 表示当前硬币不选，那么由 i - 1 种组成面值 j

    • dp[i][j - coins[i]) 表示当前硬币选了，那么还需要组成面额为 j - coins[i], 这都是已要组成的面值大于当前硬币值为前提的。

因此可以先写出一个二维 dp 的代码，再进一步进行优化，状态压缩

代码 二维 dp

public int waysToChange(int n) {
        int[] coins = new int[]{1, 5, 10, 25};
        // 1. dp 表示对应的方法数 比如 dp[i][j] 表示 i 种硬币组成面值为 j 时的方法数
        // 2. 多开一个位置，0 空着不用 在下面对dp[0][j] dp[i][0] 做特殊处理
        int[][] dp = new int[5][n + 1];//
        // 对dp[0][j] dp[i][0] 做特殊处理  且dp[0][j] 不存在
        for (int i = 1; i <= 4; i++)
            dp[i][0] = 1;
        for (int i = 1; i <= 4; i++) { // i表示 i种币值，正好也对于coins
            for (int j = 1; j <= n; n++) {// j表示 组成的面值
                if (j - coins[i - 1] < 0) // 要组成的面值比当前硬币金额小，该硬币不可以选择
                    dp[i][j] = dp[i - 1][j] % 1000000007; // 只能由 i - 1 中硬币来组成面值 j
                else
                    dp[i][j] = (dp[i - 1][j] + dp[i][j - coins[i - 1]]) % 1000000007;
            }
        }

        return dp[4][n];
    }

代码 一维 dp

public int waysToChange(int n) {
        int[] coins = new int[]{1, 5, 10, 25};
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int coin : coins) {
            for (int i = 1; i <= n; i++) {
                if (i - coin >= 0) {
                    dp[i] = (dp[i] + dp[i - coin]) % 1000000007; // sum = sum+ 1 第一个sum 和第一个sum 相差一个状态
                }
            }
        }
        return dp[n];
    }

Read more

  • Apr 26, 2020
  • 0 views

5393. 可获得的最大点数

  • 难度：中等
  • 本题涉及算法： 前缀和 滑动窗口 深度优先搜索(DFS)
  • 思路：前缀和 滑动窗口 深度优先搜索(DFS)
  • 类似题型：

题目 5393. 可获得的最大点数

几张卡牌 排成一行，每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。

每次行动，你可以从行的开头或者末尾拿一张卡牌，最终你必须正好拿 k 张卡牌。

你的点数就是你拿到手中的所有卡牌的点数之和。

给你一个整数数组 cardPoints 和整数 k，请你返回可以获得的最大点数。

示例

示例 1：

输入：cardPoints = [1,2,3,4,5,6,1], k = 3
输出：12
解释：第一次行动，不管拿哪张牌，你的点数总是 1 。但是，先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌，最终点数为 1 + 6 + 5 = 12 。

示例 2：

输入：cardPoints = [2,2,2], k = 2
输出：4
解释：无论你拿起哪两张卡牌，可获得的点数总是 4 。

示例 3：

输入：cardPoints = [9,7,7,9,7,7,9], k = 7
输出：55
解释：你必须拿起所有卡牌，可以获得的点数为所有卡牌的点数之和。

示例 4：

输入：cardPoints = [1,1000,1], k = 1
输出：1
解释：你无法拿到中间那张卡牌，所以可以获得的最大点数为 1 。

示例 5：

输入：cardPoints = [1,79,80,1,1,1,200,1], k = 3
输出：202

提示：

1 <= cardPoints.length <= 10^5
1 <= cardPoints[i] <= 10^4
1 <= k <= cardPoints.length

解题思路 sum = left + right

  • 先求的右边k个数总和
  • 在用 sum = left + right 遍历k次;
  • 比较每次大小

代码

class Solution {
    public int maxScore(int[] cardPoints, int k) {
        int max = 0;
        int rightsum = 0;
        for (int c=cardPoints.length-1;c>=cardPoints.length - k;c--) {
            rightsum += cardPoints[c];
        }
        max = rightsum;

        int leftsum = 0;
        for (int i=0;i<k;i++) {
            leftsum +=  cardPoints[i];
            rightsum = rightsum - cardPoints[cardPoints.length - k+i];
            max = Math.max(max,rightsum+leftsum);
        }
        return max;
    }
}

解题思路二 滑动窗口

  • 滑动窗口，维护一个 len-k 的窗口，保证窗口里面和最小，然后剩余的k个数的和就是最大

代码

class Solution {
    public int maxScore(int[] cardPoints, int k) {
        int len = cardPoints.length, sum = 0;
        for (int cardPoint: cardPoints) {
            sum += cardPoint;
        }
        int min = Integer.MAX_VALUE, temp = 0;
        int length = len - k;
        for (int i = 0; i < len; i++) {
            temp += cardPoints[i];
            if (i >= length) {
                temp -= cardPoints[i - length];
            }
            if (i >= length - 1)
                min = Math.min(min, temp);
        }
        return sum - min;
    }
}

解题思路三 深度优先搜索(DFS)

从最开始的节点出发，要么选左，要么选右，选择了一边之后如果还能选，那再继续上述过程，这不就是一棵树，然后就按dfs写的，但在用例较长的情况下超时了，只通过了 15/40 的样例。思路1只是提供一种思考的思路，耗时过多，没法通过本题。

public int maxScoredfs(int[] cardPoints, int k) {
        int max = 0;
        if (k == cardPoints.length) {
            for (int num : cardPoints) {
                max += num;
            }
        }

        int scores = 0;
        max = dfscard(cardPoints, k, 0, cardPoints.length - 1, scores);

        return max;
    }

    public int dfscard(int[] cardPoints, int k, int l, int r, int scores) {
        if (k == 1) // 边界条件，只能选一次的话，就选左或者右中的较大者
            return Math.max(cardPoints[l], cardPoints[r]);
        int l_max = dfscard(cardPoints, k - 1, l + 1, r, scores) + cardPoints[l];// 选择左边的情况，并继续向下dfs
        int r_max = dfscard(cardPoints, k - 1, l, r - 1, scores) + cardPoints[r];// 选择右边的情况，并继续向下dfs
        return Math.max(l_max, r_max); // 返回选左或者选右的较大者
    }

Read more

  • Apr 26, 2020
  • 0 views

5392. 分割字符串的最大得分

  • 难度：中等
  • 本题涉及算法：深度优先搜索(DFS)
  • 思路：分割字符串 线性扫描
  • 类似题型：

题目 5392. 分割字符串的最大得分

给你一个由若干 0 和 1 组成的字符串 s ，请你计算并返回将该字符串分割成两个 非空 子字符串（即 左 子字符串和 右 子字符串）所能获得的最大得分。

「分割字符串的得分」为 左 子字符串中 0 的数量加上 右 子字符串中 1 的数量。

 

示例

示例 1：

输入：s = "011101"
输出：5
解释：
将字符串 s 划分为两个非空子字符串的可行方案有：
左子字符串 = "0" 且 右子字符串 = "11101"，得分 = 1 + 4 = 5
左子字符串 = "01" 且 右子字符串 = "1101"，得分 = 1 + 3 = 4
左子字符串 = "011" 且 右子字符串 = "101"，得分 = 1 + 2 = 3
左子字符串 = "0111" 且 右子字符串 = "01"，得分 = 1 + 1 = 2
左子字符串 = "01110" 且 右子字符串 = "1"，得分 = 2 + 1 = 3

示例 2：

输入：s = "00111"
输出：5
解释：当 左子字符串 = "00" 且 右子字符串 = "111" 时，我们得到最大得分 = 2 + 3 = 5
示例 3：

输入：s = "1111"
输出：3

提示：

2 <= s.length <= 500
字符串 s 仅由字符 '0' 和 '1' 组成。

解题思路一 分割字符串

代码

class Solution {
    public int maxScore(String s) {
        int zeroCount = count(s,"0",0);
        int oneCount = count(s,"1",1);
        int max = 0;
        for (int i=1;i<s.length();i++) {
            int zero = zeroCount -  count(s,"0",i);// 总0出现个数-后面0出现个数
            int one  = count(s,"1",i);// 后面1出现的个数
            max = Math.max(max,zero+one);
        }
        return max;
    }

    public int count(String str,String target,int fromIndex) {
        int count = 0;
        while (true){
            int index = str.indexOf(target,fromIndex);
            if (index!=-1) {
                fromIndex = index +1;
                count ++;
            }else {
                break;
            }
        }
        return count;
    }
}

解题思路二 java 线性扫描O(N)

代码

class Solution {
    public int maxScore(String s) {
        int res = 0, cnt1 = 0, cnt0 = 0;        //cnt1统计右边1的个数，同理cnt0左边0的个数
        for(int i = 0; i < s.length(); i++){
            cnt1 += s.charAt(i)-'0';            //先统计1的个数
        }                                       //由于左右区域的数至少为1，所以i不能等于len-1
        for(int i = 0; i < s.length()-1; i++){  //点i分为左右两个区域        
            if(s.charAt(i) == '0') cnt0++;      //遇到01就统计，动态更新左右区域01个数
            else cnt1--;
            res = Math.max(res, cnt0+cnt1);
        }
        return res;

    }

}

Read more

  • Apr 26, 2020
  • 0 views
Search